Question

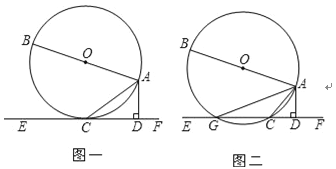
【题目】如图一，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D．

（1）求证：∠CAD=∠BAC；

（2）如图二，若把直线EF向上移动，使得EF与⊙O相交于G，C两点（点C在点G的右侧），连接AC，AG，若题中其他条件不变，这时图中是否存在与∠CAD相等的角？若存在，找出一个这样的角，并证明；若不存在，说明理由．

Answer 1

【答案】（1）∠CAD=∠BAC；

（2）∠CAD=∠BAG．

【解析】

试题分析：（1）连接OC，根据切线的性质定理以及等角的余角相等即可证明；

（2）构造直径所对的圆周角，根据等弧所对的圆周角相等以及等角的余角相等，发现∠BAC=∠GAD，再根据等式的性质即可证明∠BAG=∠DAC．

试题解析：（1）证明：如图一，连接OC，则OC⊥EF，且OC=OA，

易得∠OCA=∠OAC．

∵AD⊥EF，

∴OC∥AD．

∴∠OCA=∠CAD，

∴∠CAD=∠OAC．

即∠CAD=∠BAC．

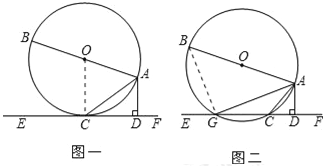
（2）解：与∠CAD相等的角是∠BAG．

证明如下：

如图二，连接BG．

∵四边形ACGB是⊙O的内接四边形，

∴∠ABG+∠ACG=180°．

∵D，C，G共线，

∴∠ACD+∠ACG=180°．

∴∠ACD=∠ABG．

∵AB是⊙O的直径，

∴∠BAG+∠ABG=90°

∵AD⊥EF

∴∠CAD+∠ACD=90°

∴∠CAD=∠BAG．