题目内容
【题目】如图，在△ABC中，∠ABC=45°，AD⊥BC于点D，点E在AD上，且DE=DC． 
（1）求证：△BDE≌△ADC；
（2）若BC=8.4，tanC= 
，求DE的长．
【答案】
（1）证明：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵∠ABC=45°，
∴∠BAD=45°，
∴∠ABC=∠BAD，
∴AD=BD，
在△BDE和△ADC中，
，
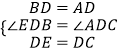∴△BDE≌△ADC（SAS）；
（2）解：设DE=x，
∵DE=DC，
∴DC=x，
∵tanC= 
，
∴AD=2.5x，
∵AD=BD，
∴BD=2.5x，
∴BC=BD+CD=3.5x，
∵BC=8.4，
∴x=2.4，
DE=2.4．
【解析】（1）由AD⊥BC可得∠ADB=∠ADC=90°，又∠ABC=45°易得∠ABC=∠BAD，可得AD=BD，由SAS定理可得△BDE≌△ADC；（2）设DE=x，因为tanC= 可得AD=2.5x，可得BC=3.5x，由BC=8.4，可解得x，可得DE．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
