题目内容
已知△ABC中,AC=BC=3 ,∠C=90°,AB上有一动点P,过P作PE⊥AC于E,PF⊥BC于F.
,∠C=90°,AB上有一动点P,过P作PE⊥AC于E,PF⊥BC于F.
(1)设CF=x,用含x的代数式把Rt△AEP、Rt△PFB及矩形ECFP的面积表示出来;
(2)是否存在这样的P点,使Rt△AEP、Rt△PFB及矩形ECFP的面积都小于4.
 解:(1)△AEP的面积为
解:(1)△AEP的面积为 ,
,△PFB的面积为
 ;
;矩形ECFP的面积为x(
 ).
).(2)设y1=
 x2,y2=x(
x2,y2=x( ),y3=
),y3= (
( )2
)2这三个二次函数的图象如图所示,令
 ,
,得x1=0,x2=2
 ;
;当x1=0时,y1=y2=0;当x2=2
 时,y1=y2=4;
时,y1=y2=4;∴y1和y2的交点坐标为O(0,0),A(2
 ,4).
,4).
由图知,在
 中,y1≥4,
中,y1≥4,由x(
 )=
)= (
( )2
)2得x3=
 ,x4=3
,x4=3 ;
;当x3=
 时,y2=y3=4,
时,y2=y3=4,当x4=3
 时,y2=y3=0,
时,y2=y3=0,∴y2和y3的交点坐标为B(
 ),C(
),C( ),
),由图知,在
 时,y3≥4,
时,y3≥4,在
 时,y2≥4,
时,y2≥4,∴在0<x<3
 中,y1,y2,y3中最大面积都不小于4,
中,y1,y2,y3中最大面积都不小于4,因此不存在这样的点P,使得三个图形的面积都小于4.
分析:(1)由于△ABC是等腰Rt△,那么∠A=∠B=45°,由此可得△AEP、△BPF也是等腰Rt△,因此此题中相等的线段有AE=PE=CF=x,BF=PF=CE=3
 -x,已知了这些线段的长,即可根据各自的面积公式进行解答.
-x,已知了这些线段的长,即可根据各自的面积公式进行解答.(2)在直角坐标系中作出三个二次函数的图象,结合图象,令两函数关系式相等,求出x、y的值,再依据x的取值范围,求y的范围,进而判断面积是否小于4.
点评:本题二次函数的综合题,要求会求两图象的交点,结合图象解决问题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( )
12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( ) 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: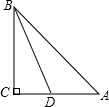 如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD.
如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD. 已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.
已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.