题目内容
已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
(1)如图1.若点P与点C重合,则
=
=
(直接写出结果):
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出
=
.

(1)如图1.若点P与点C重合,则
| AM |
| MN |
1
1
,| MC |
| AP |
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出
| MC |
| AP |
| 1 |
| 2 |
| 1 |
| 2 |

分析:(1)先求出∠C=∠CBN,再利用“角角边”证明△ACM和△NBM全等,根据全等三角形对应边相等可得AM=MN,MC=MB,再求出AP=AC=2MC,然后求解即可;
(2)过点N作NE⊥BC于E,根据同角的余角相等求出∠PBC=∠BNE,然后利用“角角边”证明△PBC和△BNE全等,根据全等三角形对应边相等可得BE=PC,NE=BC,然后求出AP=CE,AC=NE,再利用“角角边”证明△ACM和△NEM全等根据全等三角形对应边相等可得MC=ME,整理即可得证;
(3)过点N作NE⊥BC交CB的延长线于E,然后与(2)的求解方法相同.
(2)过点N作NE⊥BC于E,根据同角的余角相等求出∠PBC=∠BNE,然后利用“角角边”证明△PBC和△BNE全等,根据全等三角形对应边相等可得BE=PC,NE=BC,然后求出AP=CE,AC=NE,再利用“角角边”证明△ACM和△NEM全等根据全等三角形对应边相等可得MC=ME,整理即可得证;
(3)过点N作NE⊥BC交CB的延长线于E,然后与(2)的求解方法相同.
解答:(1)解:∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠CBN=90°,BC=BN,
∴∠C=∠CBN,AC=BN,
在△ACM和△NBM中,
,
∴△ACM≌△NBM(AAS),
∴AM=MN,MC=MB,
∴AP=AC=BC=MC+MB=2MC,
∴
=1,
=
;
 (2)证明:如图2,过点N作NE⊥BC于E,
(2)证明:如图2,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC-PC=BC-BE=CE,AC=NE,
在△ACM和△NEM中,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∴CE=2MC,
∴AP=2MC;
(3)解:如图3,过点N作NE⊥BC交CB的延长线于E,
过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC-PC=BC-BE=CE,AC=NE,
在△ACM和△NEM中,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∵AP=AC+PC,
CE=BC+BE=2MC,
∴AP=CE=2MC,
∴
=
.
故答案为:(1)1,
;(3)
.
∴∠CBN=90°,BC=BN,
∴∠C=∠CBN,AC=BN,
在△ACM和△NBM中,
|
∴△ACM≌△NBM(AAS),
∴AM=MN,MC=MB,
∴AP=AC=BC=MC+MB=2MC,
∴
| AM |
| MN |
| MC |
| AP |
| 1 |
| 2 |
 (2)证明:如图2,过点N作NE⊥BC于E,
(2)证明:如图2,过点N作NE⊥BC于E,∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,
|
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC-PC=BC-BE=CE,AC=NE,
在△ACM和△NEM中,
|
∴△ACM≌△NEM(AAS),
∴MC=ME,
∴CE=2MC,
∴AP=2MC;
(3)解:如图3,过点N作NE⊥BC交CB的延长线于E,
过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,
|
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC-PC=BC-BE=CE,AC=NE,
在△ACM和△NEM中,
|
∴△ACM≌△NEM(AAS),
∴MC=ME,
∵AP=AC+PC,
CE=BC+BE=2MC,
∴AP=CE=2MC,
∴
| MC |
| AP |
| 1 |
| 2 |
故答案为:(1)1,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判定方法与性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( )
12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( ) 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: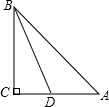 如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD.
如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD. 已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.
已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.