题目内容

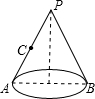精英家教网如图，圆锥的底面圆的半径为10cm，母线长为40cm，C为母线PA的中点，一只蚂蚁欲从点A处沿圆锥的侧面爬到点C处，则它爬行的最短距离是
 
cm．
分析：要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，进而根据“两点之间线段最短”得出结果．
解答：解：由题意知，底面圆的直径AB=20，故底面周长等于20π
设圆锥的侧面展开后的扇形圆心角为n°
∵根据底面周长等于展开后扇形的弧长得，20π=
40πn
180
，解得n=90°
∴展开图中扇形圆心角=90°
∵根据勾股定理求得它爬行的最短距离是
402+202
=
2000
=20
5
cm
∴蚂蚁爬行的最短距离为20
5
cm
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决．
练习册系列答案
相关题目
精英家教网已知如图，圆锥的底面圆的半径为r（r＞0），母线长OA为3r，C为母线OB的中点在圆锥的侧面上，一只蚂蚁从点A爬行到点C的最短线路长为（　　）
A、
3
2
r
B、
3
3
2
r
C、
3
3
r
D、3
3
r
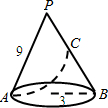精英家教网已知，如图，圆锥的底面圆的半径为3cm，母线长为9cm，C为母线PB的中点，一只蚂蚁欲从点A处沿圆锥的侧面爬到C处，则它爬行最短距离为
 
．
如图甲，已知在⊙O中，AB=4
3
，AC是⊙O的直径，AC⊥BD于F，∠A=30度．
（1）连接BC，CD，请你判定四边形OBCD是何种特殊的四边形？试说明理由；
（2）若用扇形OBD围成一个圆锥侧面，请出这个圆锥的底面圆的半径；
（3）如图乙，若将“∠A=30°”改为“∠A=22.5°”，其余条件不变，以半径OB、OD的中点M、N为顶点作矩形MNGH，顶点G、H在⊙O的劣弧
BD
上，GH交OC于点E．试求图中阴影部分的面积．（结果保留π）
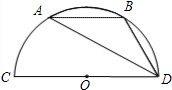精英家教网
精英家教网如图，CD是半圆O的直径，弦AB∥CD，且CD=6，∠ADB=30°，则∠AOB=
 
°，若用扇形AOB围成一个圆锥，则该圆锥的底面圆的半径为
 
．
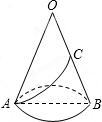已知如图，圆锥的底面圆的半径为r（r＞0），母线长OA为2r，C为母线OB的中点．在圆锥的侧面上，一只蚂蚁从点A爬行到点C的最短线路长为
5
r
5
r
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网