题目内容
将一张长方形纸片按如右图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为
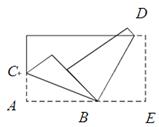
- A.60°
- B.75°
- C.90°
- D.95°
C
试题分析:根据折叠的性质得到∠ABC=∠A′BC,∠EBD=∠E′BD,再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°,易得A′BC+∠E′BD=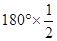 =90°,即可得到结果.
=90°,即可得到结果.
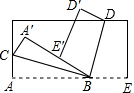
∵一张长方形纸片沿BC、BD折叠,
∴∠ABC=∠A′BC,∠EBD=∠E′BD,
而∠ABC+∠A′BC+∠EBD+∠E′BD=180°,
∴∠A′BC+∠E′BD=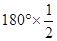 =90°,
=90°,
即∠CBD=90°.
故选C.
考点:本题考查了折叠的性质,平角的定义
点评:解答本题的关键是熟练掌握折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.
试题分析:根据折叠的性质得到∠ABC=∠A′BC,∠EBD=∠E′BD,再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°,易得A′BC+∠E′BD=
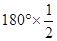 =90°,即可得到结果.
=90°,即可得到结果.
∵一张长方形纸片沿BC、BD折叠,
∴∠ABC=∠A′BC,∠EBD=∠E′BD,
而∠ABC+∠A′BC+∠EBD+∠E′BD=180°,
∴∠A′BC+∠E′BD=
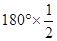 =90°,
=90°,即∠CBD=90°.
故选C.
考点:本题考查了折叠的性质,平角的定义
点评:解答本题的关键是熟练掌握折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.

练习册系列答案
相关题目
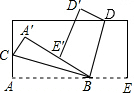 将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为
将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为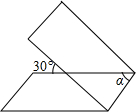 将一张长方形纸片按如图所示的方式折叠,纸带重叠部分中的∠α的度数等于( )
将一张长方形纸片按如图所示的方式折叠,纸带重叠部分中的∠α的度数等于( )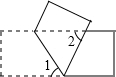 将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2等于( )
将一张长方形纸片按如图所示折叠,如果∠1=58°,那么∠2等于( )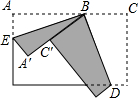 将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=35°则∠DBC为
将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠ABE=35°则∠DBC为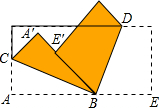 将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,求∠CBD度数.
将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,求∠CBD度数.