题目内容
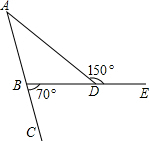
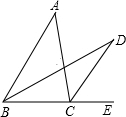
如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=______.


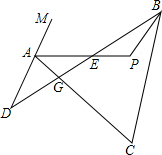
∵∠P=180°-∠PBE-∠PEB,
∠PBE=
(180°-∠C-∠CGB)①,
∠PEB=180°-∠D-∠DAE②,
∠EAG=
(180°-∠DAG)③
∴∠P=180°-∠PBE-∠PEB
=180°-
(180°-∠C-∠CGB)-∠PEB
=90°+
∠C+
∠CGB-(180°-∠D-∠DAE)
=
∠C+
∠CGB-90°+∠D+(∠DAG+
∠CAM)
=
∠C+
∠CGB-90°+∠D+(180°-∠D-∠DGA)+
(∠D+∠DGA)
=90°+
∠C+
∠D
=90°+
×62°+
×30°
=136°.
故答案为:136°.
∠PBE=
| 1 |
| 2 |
∠PEB=180°-∠D-∠DAE②,
∠EAG=
| 1 |
| 2 |
∴∠P=180°-∠PBE-∠PEB
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
| 1 |
| 2 |
=136°.
故答案为:136°.


练习册系列答案
相关题目