题目内容
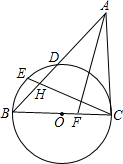
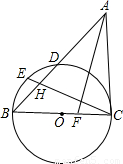
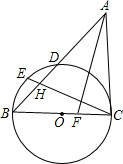 已知:如图,AF为△ABC的角平分线,以BC为直径的圆与边AB交于点D,点E为弧BD的中点,连接CE交AB于H,AH=AC.
已知:如图,AF为△ABC的角平分线,以BC为直径的圆与边AB交于点D,点E为弧BD的中点,连接CE交AB于H,AH=AC.(1)求证:AC与⊙O相切;
(2)若AC=6,AB=10,求EC的长.
分析:(1)连接BE,由AH=AC,得∠AHC=∠ACH,又∠AHC=∠EHB,所以,∠EHB=∠ACH,又由点E为弧BD的中点,所以,∠ECB=∠DBE,所以,∠ECB+∠ACH=90°,即可证明;
(2)由题意得,AC=6,AB=10,所以,BC=8,易证△BEH∽△CEB,可得,
=
=
=
,在Rt△EBC中,根据勾股定理可求得结论;
(2)由题意得,AC=6,AB=10,所以,BC=8,易证△BEH∽△CEB,可得,
| BE |
| EC |
| BH |
| CB |
| 4 |
| 8 |
| 1 |
| 2 |
解答:(1)证明:连接BE
∵BC为直径∴∠E=90°,
∴∠EBH+∠EHB=90°,
∵AH=AC,AF为△ABC的角平分线,
∴∠AHC=∠ACH,
∵∠AHC=∠EHB,
∴∠EHB=∠ACH,
∵点E为弧BD的中点,
∴∠ECB=∠DBE,
∴∠ECB+∠ACH=90°,
∴AC是⊙O的切线;
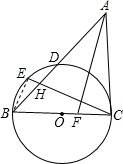
(2)解:∵AC是⊙O的切线,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC=8,
∵AH=AC,
∴BH=4,
又∵∠ECB=∠DBE,∠E为公共角,
∴△BEH∽△CEB,
∴
=
=
=
,
∴在Rt△EBC中,可得EC2+(
EC)2=BC2,
∴EC=
.
∵BC为直径∴∠E=90°,
∴∠EBH+∠EHB=90°,
∵AH=AC,AF为△ABC的角平分线,
∴∠AHC=∠ACH,
∵∠AHC=∠EHB,
∴∠EHB=∠ACH,
∵点E为弧BD的中点,
∴∠ECB=∠DBE,
∴∠ECB+∠ACH=90°,
∴AC是⊙O的切线;

(2)解:∵AC是⊙O的切线,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC=8,
∵AH=AC,
∴BH=4,
又∵∠ECB=∠DBE,∠E为公共角,
∴△BEH∽△CEB,
∴
| BE |
| EC |
| BH |
| CB |
| 4 |
| 8 |
| 1 |
| 2 |
∴在Rt△EBC中,可得EC2+(
| 1 |
| 2 |
∴EC=
16
| ||
| 5 |
点评:本题考查了勾股定理、相似三角形及切线的判定与性质的综合应用,应熟练掌握其判定、性质定理,考查了学生综合应用知识的能力.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
 点E,AE=2,ED=4.
点E,AE=2,ED=4.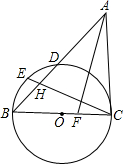 已知:如图,AF为△ABC的角平分线,以BC为直径的圆与边AB交于点D,点E为弧BD的中点,连接CE交AB于H,AH=AC.
已知:如图,AF为△ABC的角平分线,以BC为直径的圆与边AB交于点D,点E为弧BD的中点,连接CE交AB于H,AH=AC.