题目内容
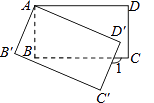
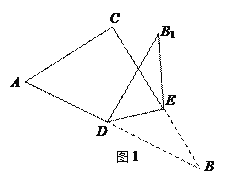
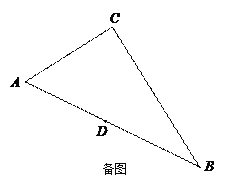
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.


【答案】(1)![]() 或3;(2)
或3;(2)![]() .
.
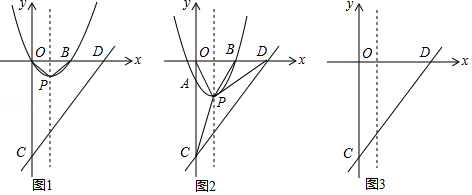
【解析】(1)如图1,由平行四边形的性质得DB1∥AC,且DB1=AC=3,由折叠知BD=DB1= 3,∠BDE=∠EDB1==30°,过E作EH⊥DB于H,则DH=BH=![]() ,在Rt△DEH中,根据勾股定理得DE2=(
,在Rt△DEH中,根据勾股定理得DE2=(![]() DE)2+
DE)2+![]() ,解之可得DE的值;如图2,由平行四边形的性质得B1D∥AC,且B1D=AC=3,又CD=
,解之可得DE的值;如图2,由平行四边形的性质得B1D∥AC,且B1D=AC=3,又CD=![]() AB=3,∠CAB=60°,可证四边形ACDB1为含60°角的菱形,从而∠E B1D=∠C B1D =30°,即E与C重合,DE的长即是CD的长.
AB=3,∠CAB=60°,可证四边形ACDB1为含60°角的菱形,从而∠E B1D=∠C B1D =30°,即E与C重合,DE的长即是CD的长.
(2)设B1D、B1E分别与AC交于P、Q,在Rt△ADP中,求出AP和DP的长,在Rt△B1PQ中,求出B 1P和PQ的长,然后根据△DE B1和△ABC重叠部分的面积=S△B1DE- S△B1PQ计算即可.
(1)如图1,若四边形为ACB1D的平行四边形,则有DB1∥AC,且DB1=AC=3,
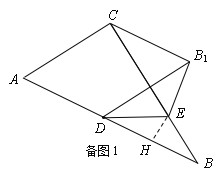
由题意,∠B=30°,∠BDE=∠EDB1=30°,
∴DE=BE,
在Rt△ABC中,∠A=60°,AC=3,∴AB=6,BD=3,
过E作EH⊥DB于H,则DH=BH=![]() ,
,
在Rt△DEH中,EH=![]() DE,DH=
DE,DH=![]() ,
,
∴DE2=(![]() DE)2+
DE)2+![]() ,
,
∴DE=![]() ;
;
如图2,若四边形为ACDB1的平行四边形,则有,B1D∥AC,且B1D=AC=3,

∵CD=![]() AB=3,∠CAB=60°,
AB=3,∠CAB=60°,
∴四边形ACDB1为含60°角的菱形,
∵∠E B1D=∠C B1D =30°,
∴E与C重合,
∴DE=CD=3;
综上,DE=![]() 或3,
或3,
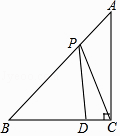
(2)当DB1⊥AC时(如图3),设B1D、B1E分别与AC交于P、Q,
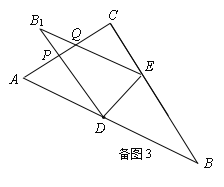
则:Rt△ADP中,∠A=60°,AD=3,
∴AP=![]() ,DP=
,DP=![]()
![]() ,
,
Rt△B1PQ中,∠B 1=∠B=30°,B 1P=3-![]()
![]() ,
,
∴PQ=![]() -
-![]() ,
,
∴S△B1PQ=![]() ×B 1P
×B 1P![]() PQ=
PQ=![]() ×(3-
×(3-![]()
![]() )(
)(![]() -
-![]() )=
)=![]() -
-![]() ,
,
又S△B1DE==![]() ×DB 1
×DB 1![]() PC=
PC=![]() ×3×
×3×![]() =
=![]() ,
,
∴△DE B1和△ABC重叠部分的面积=![]() -
-![]() +
+![]() =
=![]() -
-![]() .
.

 阅读快车系列答案
阅读快车系列答案