��Ŀ����
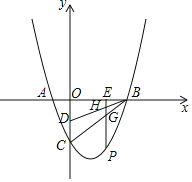
����Ŀ����֪������y��x2��2x��3��x�ύ�ڵ�A��B����y�ύ�ڵ�C����DΪOC�е㣬��P���������ϣ�
��1��ֱ��д��A��B��C��D���ꣻ
��2����P�ڵ������ޣ�����P��PE��x�ᣬ����ΪE��PE��BC��BD��G��H���Ƿ���������ĵ�P��ʹPG��GH��HE�������ڣ������P���ꣻ�������ڣ���˵�����ɣ�
��3����ֱ��y��![]() x+t��������y��x2��2x��3��x���·����������㣬ֱ��д��t��ȡֵ��Χ��
x+t��������y��x2��2x��3��x���·����������㣬ֱ��д��t��ȡֵ��Χ��
���𰸡���1��A(��1��0)��B(3��0)��C(0����3)��D(0����![]() )����2�����ڣ�(
)����2�����ڣ�(![]() ����
����![]() )����3����
)����3����![]() ��t����1
��t����1
��������
��1����ͨ�����κ����Ľ���ʽ�г����̣����������ص�����ꣻ
��2�����ڣ������ֱ��BC��ֱ��BD�Ľ���ʽ�����P������Ϊ��x��x2��2x��3������E��x��0����H��x��![]() x��
x��![]() ����G��x��x��3�����г���ʽ���̣����������P���ꣻ
����G��x��x��3�����г���ʽ���̣����������P���ꣻ
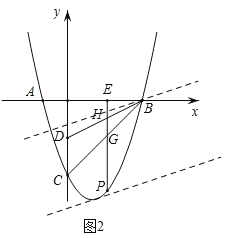
��3�����ֱ��y��![]() x+t������Bʱt��ֵ�����г���ֱ��y��
x+t������Bʱt��ֵ�����г���ֱ��y��![]() x+t��������y��x2��2x��3ֻ��һ������ʱ�ķ��̣�ʹ�����б�ʽΪ0�����t��ֵ������д��t��ȡֵ��Χ��
x+t��������y��x2��2x��3ֻ��һ������ʱ�ķ��̣�ʹ�����б�ʽΪ0�����t��ֵ������д��t��ȡֵ��Χ��
�⣺��1����y��x2��2x��3�У�
��x��0ʱ��y����3����y��0ʱ��x1����1��x2��3��
��A����1��0����B��3��0����C��0����3����
��DΪOC���е㣬
��D��0����![]() ����
����
��2�����ڣ��������£�
��ֱ��BC�Ľ���ʽΪy��kx��3��
����B��3��0������y��kx��3��
���k��1��
��ֱ��BC�Ľ���ʽΪy��x��3��
��ֱ��BD�Ľ���ʽΪy��mx��![]() ��
��
����B��3��0������y��mx��![]() ��
��
���m��![]() ��
��
��ֱ��BD�Ľ���ʽΪy��![]() x��
x��![]() ��
��
���P��������x��x2��2x��3������E��x��0����H��x��![]() x��
x��![]() ����G��x��x��3����
����G��x��x��3����
��EH����![]() x+
x+![]() ��HG��
��HG��![]() x��
x��![]() ����x��3������
����x��3������![]() x+
x+![]() ��GP��x��3����x2��2x��3������x2+3x��
��GP��x��3����x2��2x��3������x2+3x��
��EH��HG��GPʱ����![]() x+
x+![]() ����x2+3x��
����x2+3x��
���x1��![]() ��x2��3����ȥ����
��x2��3����ȥ����
���P��������![]() ����
����![]() ����
����
��3����ֱ��y��![]() x+t������Bʱ��
x+t������Bʱ��
����B��3��0������y��![]() x+t��
x+t��
�ã�t����1��
��ֱ��y��![]() x+t��������y��x2��2x��3ֻ��һ������ʱ������
x+t��������y��x2��2x��3ֻ��һ������ʱ������![]() x+t��x2��2x��3ֻ��һ���⣬
x+t��x2��2x��3ֻ��һ���⣬
��x2��![]() x��3��t��0��
x��3��t��0��
������![]() ��2��4����3��t����0��
��2��4����3��t����0��
���t����![]() ��
��
����ͼ2���Կ�������ֱ��y��![]() x+t��������y��x2��2x��3��x���·�����������ʱ��t��ȡֵ��ΧΪ����
x+t��������y��x2��2x��3��x���·�����������ʱ��t��ȡֵ��ΧΪ����![]() ��t����1ʱ��
��t����1ʱ��

 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�