题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且
,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
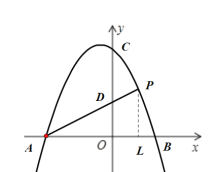
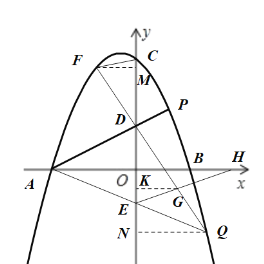
(2)如图1,点![]() 在第一象限的抛物线上,其横坐标为
在第一象限的抛物线上,其横坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() ,若
,若![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
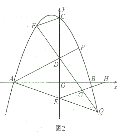
(3)如图2,在(2)的条件下,点![]() 在第四象限的抛物线上,其横坐标为
在第四象限的抛物线上,其横坐标为![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() 并延长,交抛物线于点
并延长,交抛物线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

【答案】(1)A(-6,0),B(4,0) (2)d=2t,![]() (3)5
(3)5
【解析】
(1)根据抛物线的对称轴为直线![]() ,点
,点![]() 、
、![]() 关于对称轴对称即可得到点
关于对称轴对称即可得到点![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)利用![]() 得到点C的坐标,然后将B、C两点的坐标代入
得到点C的坐标,然后将B、C两点的坐标代入![]() 求出函数的解析式,则可得到
求出函数的解析式,则可得到![]() ,则可得到
,则可得到![]() ,
,![]() ,利用
,利用![]() ,可求得
,可求得![]() ,即可得
,即可得![]() (
(![]() );
);
(3)过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,可得
,可得![]() ,
,![]() ,则有
,则有![]() ,设
,设![]() ,可得到
,可得到![]() ,所以有
,所以有![]() ,同(2)可求
,同(2)可求![]() ,可证得
,可证得![]() ,
,![]() ,可求得
,可求得![]() ,则可以求出
,则可以求出![]() .
.
(1)抛物线的对称轴为直线![]()
![]() ,点
,点![]() 、
、![]() 关于对称轴对称
关于对称轴对称
![]() 点
点![]() 、
、![]() 到对称轴的距离为
到对称轴的距离为![]()
![]() ,
,![]()
![]() ,
,![]()
∴A(-6,0),B(4,0)
(2)如图示,过![]() 作
作![]() 轴于点
轴于点![]()
![]()
![]()
![]()
![]()
把![]() 代入抛物线解析式
代入抛物线解析式![]() 得
得![]()
解得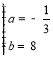
![]() 抛物线的解析式为
抛物线的解析式为![]()
![]()
![]()
![]() ,即
,即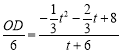
![]()
![]() (
(![]() ),
),
(3)过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,
,
则![]() ,
,![]() 轴
轴
![]() 的横坐标为
的横坐标为![]()
![]()
![]()
![]()
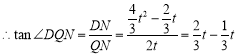
设![]()
![]()
![]()
解得![]() (舍)或
(舍)或![]()
![]()
![]()
同(2)可求![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() 轴
轴
![]()
![]()
![]()
![]()
![]()
![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目