题目内容
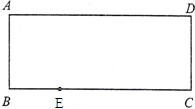 有一张矩形纸片ABCD,已知AB=2,AD=5,把这张纸片折叠,使点A落在边BC上的点E处,折痕为MN,MN交AB于M,交AD于N.
有一张矩形纸片ABCD,已知AB=2,AD=5,把这张纸片折叠,使点A落在边BC上的点E处,折痕为MN,MN交AB于M,交AD于N.(1)已知BC上的点E,试画出折痕MN的位置,并保留作图痕迹.
(2)若BE=
| 2 |
(3)当点E在BC上运动时,设BE=x,AN=y,试求y关于x的函数解析式,并写出x的取值范围.
(4)连接DE,是否存在这样的点E,使△AME与△DNE相似?若存在,请求出这时BE的长,若不存在,请说明理由.
分析:(1)连接AE,并作AE的中垂线,交AB与M、交AD与N,即可作出折痕MN;
(2)连接ME,设BM=x,则ME=2-x,由勾股定理可得:BM2+BE2=ME2,即可得方程,解方程即可求得AM的值;
(3)延长NM交CB延长线于G点,由BE=x,令BM=a,即可得a2+x2=(2-a)2,则可求得AM的值,又由△GBM∽△ANM,根据相似三角形的对应边成比例,即可求得y关于x的函数解析式;
(4)若BC上存在点E,要使△AME∽△DNE,则△ABE∽△DEC,由相似三角形的对应边成比例,即可求得BE的值.
(2)连接ME,设BM=x,则ME=2-x,由勾股定理可得:BM2+BE2=ME2,即可得方程,解方程即可求得AM的值;
(3)延长NM交CB延长线于G点,由BE=x,令BM=a,即可得a2+x2=(2-a)2,则可求得AM的值,又由△GBM∽△ANM,根据相似三角形的对应边成比例,即可求得y关于x的函数解析式;
(4)若BC上存在点E,要使△AME∽△DNE,则△ABE∽△DEC,由相似三角形的对应边成比例,即可求得BE的值.
解答: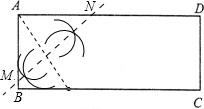 解:(1)连接AE,并作AE的中垂线,交AB与M、交AD与N.如图:(3分)
解:(1)连接AE,并作AE的中垂线,交AB与M、交AD与N.如图:(3分)
(2)连接ME,如图1,
∵BE=
,
设BM=x,则ME=2-x,
由勾股定理可得:BM2+BE2=ME2,
∴2+x2=(2-x)2,
∴2+x2=4-4x+x2,
∴x=
,
∴AM=
;
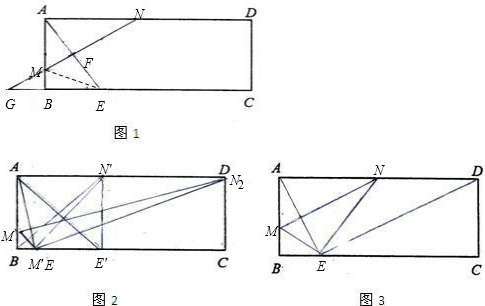
(3)延长NM交CB延长线于G点,如图2,
∵BE=x,令BM=a,
则a2+x2=(2-a)2,
a2+x2=4-4a+a2,
∴a=
,
∴AM=2-
=
,
∵AN=y,
∴GB=y-x,
∵△GBM∽△ANM,
∴
=
,
即:
=
=
,
∴y=
,(8分)
∵0<x≤2,0<y≤5,
∴5-
≤x≤2;(9分)
(4)若BC上存在点E,如图3,使△AME∽△DNE,
∵AM=ME,
∴∠MAE=∠MEA,
又∵EN=ND,
∴∠NDE=∠NED,
∵AD∥BC,
∴∠NED=∠DEC,
要使△AME∽△DNE,
则△ABE∽△DEC,
∴
=
,
∴
=
,
∴x2-5x+4=0,
解得:x1=4(舍去),x2=1,
∴BE=1,存在点E.(12分)
 解:(1)连接AE,并作AE的中垂线,交AB与M、交AD与N.如图:(3分)
解:(1)连接AE,并作AE的中垂线,交AB与M、交AD与N.如图:(3分)(2)连接ME,如图1,
∵BE=
| 2 |
设BM=x,则ME=2-x,
由勾股定理可得:BM2+BE2=ME2,
∴2+x2=(2-x)2,
∴2+x2=4-4x+x2,
∴x=
| 1 |
| 2 |
∴AM=
| 3 |
| 2 |

(3)延长NM交CB延长线于G点,如图2,
∵BE=x,令BM=a,
则a2+x2=(2-a)2,
a2+x2=4-4a+a2,
∴a=
| 4-x2 |
| 4 |
∴AM=2-
| 4-x2 |
| 4 |
| 4+x2 |
| 4 |
∵AN=y,
∴GB=y-x,
∵△GBM∽△ANM,
∴
| GB |
| AN |
| BM |
| AM |
即:
| y-x |
| y |
| ||
|
| 4-x2 |
| 4+x2 |
∴y=
| 4+x2 |
| 2x |
∵0<x≤2,0<y≤5,
∴5-
| 21 |
(4)若BC上存在点E,如图3,使△AME∽△DNE,
∵AM=ME,
∴∠MAE=∠MEA,
又∵EN=ND,
∴∠NDE=∠NED,
∵AD∥BC,
∴∠NED=∠DEC,
要使△AME∽△DNE,
则△ABE∽△DEC,
∴
| AB |
| EC |
| BE |
| CD |
∴
| 2 |
| 5-x |
| x |
| 2 |
∴x2-5x+4=0,
解得:x1=4(舍去),x2=1,
∴BE=1,存在点E.(12分)
点评:此题考查了折叠的性质,相似三角形的判定与性质,勾股定理等知识.此题综合性较强,难度较大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
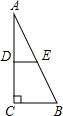 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 