题目内容
【题目】如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①∠ABE=∠ACE;②∠BCE+∠BCD=180°;③AE=EC;④BE+BD=2BF,其中正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
【答案】D
【解析】∵BD为∠ABC的角平分线,
∴∠ABE=∠CBE,
又BD=BC,BA=BE,
∴∠BCD=![]() (180°∠CBE),∠BEA=
(180°∠CBE),∠BEA=![]() (180°∠ABE),即∠BCD=∠BEA,
(180°∠ABE),即∠BCD=∠BEA,
又∠BDC=∠ADE,
∴△ADE∽△BCD,
∴![]() ,∠DAE=∠CBE,
,∠DAE=∠CBE,
∴∠ABE=∠DAE,
又∠ADB=∠EDC,
∴△ADB∽△EDC,
∴∠ACE=∠ABE,故选项①正确;
∴A、B. C.E四点共圆,
∴∠BCE+∠BAE=180°,又∠BCD=∠BAE,
∴∠BCE+∠BCD=180°,故选项②正确;
∴∠DAE=∠ACE,
∴AE=EC,故选项③正确;
过E作BC延长线的垂线,垂足为M,如图所示:
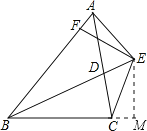
∵∠BCE+∠BAE=180°,∠BCE+∠ECM=180°,
∴∠BAE=∠ECM,
又BE为∠ABC平分线,EF⊥AB,EM⊥BM,
∴EF=EM,
在△AEF和△CEM中, 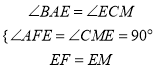 ,
,
∴△AEF≌△CEM(AAS),
∴AF=CM,又AB=EB,BC=BD,
则BE+BD=AB+BC=BF+AF+BC=BF+BC+CM=BF+BF=2BF,
故选项④正确,
则其中正确的是①②③④.
故选:D.

练习册系列答案
相关题目