��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У���DΪBC�ߵ��е㣬�Ե�DΪ����ġ�EDF�����߷ֱ����AB��AC���ڵ�E��F���ҡ�EDF���A������
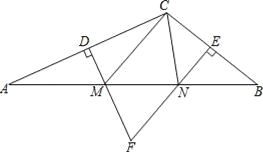
��1����ͼ1����AB=AC���ҡ�A=90�㣬���߶�DE��DF�к�������ϵ����ֱ��д�����ۣ�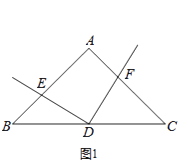
��2����ͼ2����AB=AC����ô��1���еĽ����Ƿ������������������֤����������������˵�����ɣ�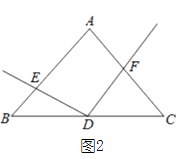
��3����ͼ3����AB��AC=m��n��̽���߶�DE��DF��������ϵ����֤����Ľ��ۣ�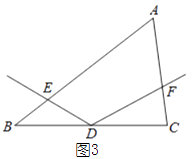
���𰸡�
��1���⣺DF=DE��
���ɣ���ͼ1������AD�� 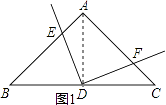
��Rt��ABC�ǵ��������Σ�
���C=��B=45�㣬
��D��б��BC���е㣬
���DAB=��DAC= ![]() ��BAC=45�㣬AD��BC��
��BAC=45�㣬AD��BC��
��AD=DC��
�ߡ�EDF=90�㣬
���ADF+��ADE=90�㣬
��AD��BC��
���ADC=90�㣬
���ADF+��FDC=90�㣬
���ADE=��FDC��
�ڡ�ADE�͡�CDF�У�  ��
��
���AED�ա�CFD��ASA����
��DE=DF��
��2���⣺DE=DF��Ȼ������
��ͼ2������D��DM��AB��M����DN��AC��N������AD��
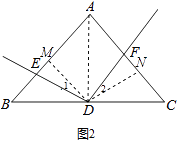
���EMD=��FND=90�㣬
��AB=AC����DΪBC�е㣬
��ADƽ�֡�BAC��
��DM=DN��
�����ı���AMDN�У�����DMA=��DNA=90�㣬
���MAN+��MDN=180�㣬
�֡ߡ�EDF���MAN������
���MDN=��EDF��
���1=��2���ڡ�DEM���DFN�У� 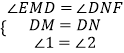 ��
��
���DEM�ա�DFN��ASA����
��DE=DF��
��3���⣺����DE��DF=n��m��
��ͼ3������D��DM��AB��M����DN��AC��N������AD��
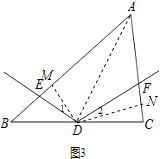
ͬ��2����֤��1=��2��
�֡ߡ�EMD=��FND=90�㣬
���DEM�ס�DFN��
�� ![]() ��
��
�ߵ�DΪBC�ߵ��е㣬
��S��ABD=S��ADC��
�� ![]() ��
��
�� ![]() ��
��
�֡� ![]() ��
��
�� ![]() ��
��
����������1��DF=DE�����ɣ���ͼ1������AD�����ݵ���ֱ�������ε����ʼ����������ε����ߺ�һ�á�C=��B=45�㣬��DAB=��DAC=45�㣬AD��BC��Ȼ�����ͬ�ǵ������ȵó���ADE=��FDC����������ASA�жϳ���AED�ա�CFD������ȫ�������ζ�Ӧ����ȵó�DE=DF��
��2��DE=DF��Ȼ��������ͼ2������D��DM��AB��M����DN��AC��N������AD�����ݵ��������ε����ߺ�һ�ó�ADƽ�֡�BAC���ٸ��ݽ�ƽ���ߵ����ʶ����ó�DM=DN�������ı��ε��ڽǺ͵ó���MAN+��MDN=180�㣬�ָ���ͬ�ǵIJ�����ȵó���MDN=��EDF�������ó���1=��2��Ȼ�����ASA�жϳ���DEM�ա�DFN������ȫ�������ζ�Ӧ����ȵó����ۣ�
��3������DE��DF=n��m����ͼ3������D��DM��AB��M����DN��AC��N������AD����AA�жϳ���DEM�ס�DFN���������������εĶ�Ӧ�߳ɱ����ó�![]() =
=![]() ,���ݵȵ�ͬ�ߵ����������������ȵó�S��ABD=S��ADC���ó��Ȼ�ʽ���ٸ��ݵ��������ó����ۡ�
,���ݵȵ�ͬ�ߵ����������������ȵó�S��ABD=S��ADC���ó��Ȼ�ʽ���ٸ��ݵ��������ó����ۡ�
�����㾫�������յ���ֱ�������κͽ�ƽ���ߵ����ʶ����ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻����1���ڽǵ�ƽ�����ϵĵ㵽����ǵ����ߵľ�����ȣ� ����2��һ���ǵ����ߵľ�����ȵĵ㣬������ǵ�ƽ�����ϣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�