题目内容
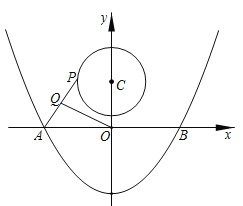
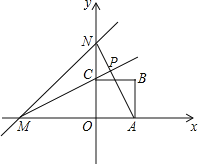
【题目】直线y=x+8分别与x轴、y轴相交于点M,N,边长为4的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则PC长度的最小值是_____.
【答案】4![]() ﹣4.
﹣4.
【解析】
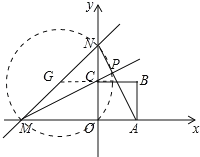
首先证明△MOC≌△NOA,推出∠MPN=90°,推出P在以MN为直径的圆上,所以当圆心G,点P,C三点共线时,PC长度的最小值.求出此时的PC即可.
在△MOC和△NOA中,
∵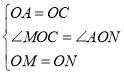 ,∴△MOC≌△NOA(SAS),∴∠CMO=∠ANO.
,∴△MOC≌△NOA(SAS),∴∠CMO=∠ANO.
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°,
∴MP⊥NP.
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上.
∵直线y=x+8分别与x轴、y轴相交于点M,N,
∴M(﹣8,0),N(0,8),
∴圆心G为(﹣4,4),半径为4![]() ,
,
∵PG﹣GC≤PC,
∴当圆心G,点P,点C三点共线时,PC最小.
∵GN=GM,CN=CO=4,∴GC![]() OM=4,
OM=4,
这个最小值为GP﹣GC=4![]() 4.
4.
故答案为:4![]() 4.
4.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目