Question

如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为点C，连接OD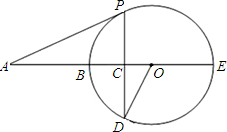，且∠AOD=∠APC．
（1）求证：AP为⊙O的切线；
（2）若OC：CB=1：2，且AB=9，求sinA的值及⊙O的半径；
（3）若点F为

PE

上任意一点（点F不与P、E两点重合），求证：△AFO∽△FCO．

Answer 1

分析：（1）连接OP，证OP⊥AP即可；可结合已知的等角和等腰三角形、直角三角形的性质进行证明．
（2）根据OC、BC的比例关系，可用未知数表示出OC、BC的表达式，进而可得OP、OB的表达式；在Rt△AOP中，PC⊥OA，根据射影定理得：PC²=PC•AC，PC²的表达式可在Rt△OPC中由勾股定理求得，由此求得未知数的知，从而确定OP、OA的长，也就能求出⊙O的半径和sinA的值．
（3）此题需要通过相似三角形来间接的证明所求的结论；在Rt△OAP中，PC⊥OA，易得△OPC∽△OAP，即可得OP：OC=OA：OP，已知OP=OB=OF，通过等量代换，可证得夹∠AOF的两组对应边成比例，根据SAS即可证得所求的结论．

解答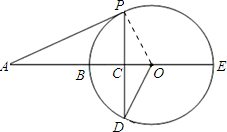：（1）证明：连接OP；
∵OP=OD，∴∠OPD=∠D；
在Rt△OCD中，∠D+∠AOD=90°，
已知∠AOD=∠APC，
则∠OPD+∠APD=90°，即OP⊥AP；
又OP是⊙O的半径，
所以AP是⊙O的切线．

（2）解：设OC=x，则BC=2x，OP=OB=3x；
在Rt△OPC中，OP=3x，OC=x，由勾股定理得：
PC²=OP²-OC²=8x²；
在Rt△OPC中，PC⊥OA，由射影定理得：
PC²=OC•AC，即8x²=x（2x+9），6x²=9x，
解得x=0（舍去），x=

3

2

；
∴OP=OB=

9

2

，OA=OB+AB=13

1

2

；
∴⊙O的半径为

9

2

，sinA=

OP

OA

=

1

3

．

（3）证明：Rt△AOP中，PC⊥OA，则有：
△OCP∽△OPA?

OP

OC

=

OA

OP

；
∵OP=OB=OF，
∴

OF

OC

=

OA

OF

；
又∵∠AOF=∠FOC，
∴△FOC∽△AOF．

点评：此题主要考查了切线的判定、等腰三角形及直角三角形的性质、以及相似三角形的判定和性质等知识，难度适中．