Question

【题目】如图，AD∥BC，AB⊥BC，CD⊥DE，CD＝ED，AD＝4，BC＝6，则△ADE的面积为（　　）

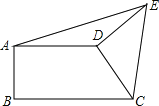
A.2B.4C.5D.无法确定

Answer 1

【答案】B

【解析】

过点D作DG⊥BC于G，过点E作EF⊥AD，交AD的延长线于点F，先证明△EDF≌△CDG（AAS），从而得EF=CG，再证明四边形ABGD为矩形，然后利用EF=CG=BC-BG=BC-AD，求得EF的值，最后利用三角形面积公式计算即可得出答案．

过点D作DG⊥BC于G，过点E作EF⊥AD，交AD的延长线于点F

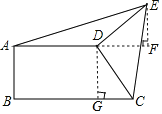
又∵CD⊥DE

∴∠EDF+∠FDC＝90°，∠GDC+∠FDC＝90°

∴∠EDF＝∠GDC

∴在△EDF和△CDG中

，

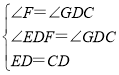∴△EDF≌△CDG（AAS）

∴EF＝CG

∵AD∥BC，AB⊥BC，DG⊥BC

∴∠BAD＝∠B＝∠DGB＝90°

∴四边形ABGD为矩形

∴BG＝AD＝4

又∵BC＝6

∴EF＝CG＝BC﹣BG＝BC﹣AD＝6﹣4＝2

△ADE的面积为：AD×EF÷2＝4×2÷2＝4

故选：B．