Question

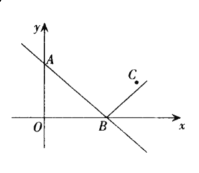
【题目】如图，若折叠矩形的一边，使点落在边的点处，已知折痕且．以为原点，所在直线为轴建立如图所示的平面直角坐标系，抛物线经过点．

(1)求的值；

(2)点是线段上一动点，点在抛物线上，且始终满足，在点运动过程中，能否使得？若能，求出所有符合条件的点的坐标；若不能，请说明理由；

(3)已知点是拋物线上一动点，点在的延长线上，且，若在轴上存在一点，使有最小值，求点的纵坐标的最大值．

Answer 1

【答案】（1）；（2）存在点，；（3）点纵坐标的最大值为．

【解析】

（1）由折叠和矩形的性质可知：∠EDB=∠BCE=90°，可证△ABD∽△ODE，从而求c；

（2）由（1）中的相似三角形可求得DA、AB，进而求出F的坐标，得BF=DF.再利用直角三角形的性质可得MD=MB，从而推导出结论；

（3）设抛物线与x轴交于M、N两点，过点D作x轴垂线交BC于点G.可求得DM=DN=DG，进而得出M、N为满足条件的点Q.

解：（1）由，设，则，，∴．

由题意，得，

∴．

∵，

∴，

∴，

∴，∴，

∴．

∵，在中，由勾股定理，得，即，

解得．∴．

∵抛物线经过点，

∴．

（2）假设存在．

由（1）知，，∴，．

∴．

易求直线BE的解析式为．

设，作PG⊥x轴于点，轴于点H．

∵，，

∴．

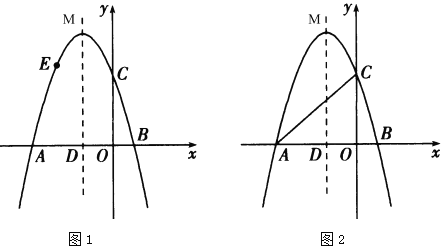
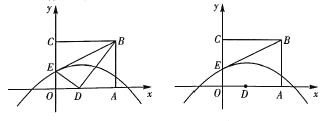
① 图1，若点在点左侧时，

则，

，，

∴．

∵点在线段BE上．

∴．

解得（舍去）或．

∴．

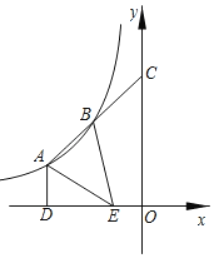
② 图2，若点在点右侧时，

则，，．

∴．

∵点在线段BE上，

∴，

解得（舍去）或．

∴

综上，存在点，，使得．

（3）∵，点在的延长线上，且，∴．

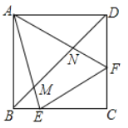
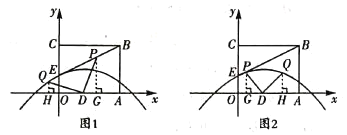
如图3，当点在轴左侧时，与轴的交点就是使得有最小值的点．

显然，当直线与抛物线只有一个公共点时，点的纵坐标最大．

设直线的解析式为y=kx+b，则，

∴，∴．

令，

即，

∴，

解得（舍去），．

∴直线的解析式为．

∴点纵坐标的最大值为．

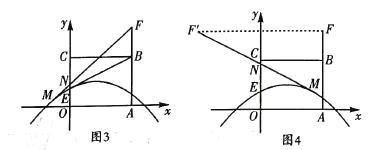
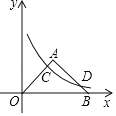
如图4，当点在轴右侧时，作点关于轴的对称点，则．连接交轴于点，则点就是使得有最小值的点．

显然，当直线与抛物线只有一个公共点时，点的纵坐标最大．设直线的解析式为y=kx+b，则．

∴，∴．

令，

即，

∴，

解得（舍去），．

∴直线的解析式为．

∴点的纵坐标的最大值为．

∵，∴，∴，

∴点纵坐标的最大值为．