题目内容
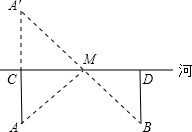
如图，牧童在A处放牛，其家在B处，A、B到河岸的距离分别为AC和BD，且AC=BD，若点A到河岸CD的中点的距离为500米，则牧童从A处把牛牵到河边饮水再回家，最短距离是（ ）
| A．750米 | B．1000米 | C．1500米 | D．2000米 |
作A关于CD的对称点A′，连接A′B，交CD于M，
∴CA′=AC，
∵AC=DB，
∴CA′=BD，
由分析可知，点M为饮水处，
∵AC⊥CD，BD⊥CD，
∴∠ACD=∠A′CD=∠BDC=90°，
又∵∠A′MC=∠BMD，
在△CA′M和△DBM中，
，
∴△CA′M≌△DBM（AAS），
∴A′M=BM，CM=DM，
即M为CD中点，
∴AM=BM=A′M=500，
所以最短距离为2AM=2×500=1000米，
故选B．
∴CA′=AC，
∵AC=DB，
∴CA′=BD，
由分析可知，点M为饮水处，
∵AC⊥CD，BD⊥CD，
∴∠ACD=∠A′CD=∠BDC=90°，
又∵∠A′MC=∠BMD，
在△CA′M和△DBM中，
|
∴△CA′M≌△DBM（AAS），
∴A′M=BM，CM=DM，
即M为CD中点，
∴AM=BM=A′M=500，
所以最短距离为2AM=2×500=1000米，
故选B．
练习册系列答案
备战中考寒假系列答案
相关题目
