题目内容
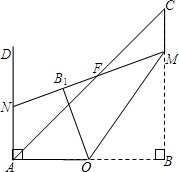 (2012•虹口区二模)如图,△ABC中,∠ABC=90°,AB=BC=4,点O为AB边的中点,点M是BC边上一动点(不与点B、C重合),AD⊥AB,垂足为点A.连接MO,将△BOM沿直线MO翻折,点B落在点B1处,直线M B1与AC、AD分别交于点F、N.
(2012•虹口区二模)如图,△ABC中,∠ABC=90°,AB=BC=4,点O为AB边的中点,点M是BC边上一动点(不与点B、C重合),AD⊥AB,垂足为点A.连接MO,将△BOM沿直线MO翻折,点B落在点B1处,直线M B1与AC、AD分别交于点F、N.(1)当∠CMF=120°时,求BM的长;
(2)设BM=x,y=
| △CMF的周长 | △ANF的周长 |
(3)连接NO,与AC边交于点E,当△FMC和△AEO相似时,求BM的长.
分析:(1)根据翻折变换的性质得出,当∠CMF=120°时,∠BMO=30°,再利用MB=
求出即可;
(2)首先得出△ANO≌△B1NO,进而得出△MB1O∽△OB1N,△CMF∽△ANF,利用相似三角形的性质得出
=
=
=
,即可得出答案;
(3)根据△FMC和△AEO相似得出有两种情况即:当△FMC∽△AEO时或当△FMC∽△AOE时,分别利用相似三角形的性质以及解直角三角形求出即可.
| BO |
| tan30° |
(2)首先得出△ANO≌△B1NO,进而得出△MB1O∽△OB1N,△CMF∽△ANF,利用相似三角形的性质得出
| C△CMF |
| C△ANF |
| CM |
| AN |
| 4-x | ||
|
| 4x-x2 |
| 4 |
(3)根据△FMC和△AEO相似得出有两种情况即:当△FMC∽△AEO时或当△FMC∽△AOE时,分别利用相似三角形的性质以及解直角三角形求出即可.
解答: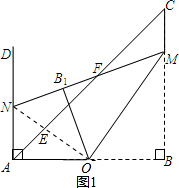 解:(1)当∠CMF=120°时,
解:(1)当∠CMF=120°时,
∵将△BOM沿直线MO翻折,点B落在点B1处,
∴∠BMO=∠OMB1,
∵∠CMF=120°,
∴∠BMO=30°,
∵AB=BC=4,点O为AB边的中点,
∴BO=2,
∴Rt△MOB中,MB=
=
=2
,;
(2)连接ON,
由(1)可得:
在Rt△ANO和Rt△B1NO中,
∵
∴△ANO≌△B1NO(HL),
∴∠AON=∠B1ON,AN=NB1,
又∵∠MOB1=∠MOB,
∴∠NOM=90°,
∴∠OMN=∠NOB1,
又∵∠OB1M=∠OB1N=∠B=90°,
∴△MB1O∽△OB1N,
∴
=
∴OB12=MB1•NB1,
又∵MB1=MB=x,OB1=OB=2,
∴22=x•NB1,
∴NB1=
,
∴AN=
,
∵AD⊥AB,
∴∠DAB=90°,
又∵∠B=90°,
∴AD∥BC,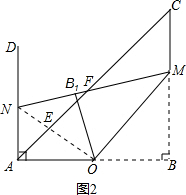
∴△CMF∽△ANF,
∴
=
=
=
=-
x2+x,
∴y=-
x2+x(0<x<4);
(3)由题意知:∠EAO=∠C=45°
∵△FMC和△AEO相似,
∴只有两种情况:当△FMC∽△AEO时或当△FMC∽△AOE时,
①如图2,当△FMC∽△AEO时,有∠FMC=∠AEO,∠CFM=∠AOE,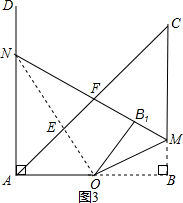
可证:∠AOE=∠OMB=∠FMO,
则∠CFM=∠FMO,
∴OM∥AC,
∴∠OMB=∠C=45°,
∴Rt△MOB中,MB=OB•tan45°=2,
②如图3,当△FMC∽△AOE时,
则∠FMC=∠AOE,
∵∠AOE=∠OMB=∠OMF,
∴∠CMF=∠OMF=∠OMB=60°,
∴Rt△MOB中,MB=
=
,
所以,综上述,知BM=2或BM=
.
 解:(1)当∠CMF=120°时,
解:(1)当∠CMF=120°时,∵将△BOM沿直线MO翻折,点B落在点B1处,
∴∠BMO=∠OMB1,
∵∠CMF=120°,
∴∠BMO=30°,
∵AB=BC=4,点O为AB边的中点,
∴BO=2,
∴Rt△MOB中,MB=
| BO |
| tan30° |
| 2 | ||||
|
| 3 |
(2)连接ON,
由(1)可得:
在Rt△ANO和Rt△B1NO中,
∵
|
∴△ANO≌△B1NO(HL),
∴∠AON=∠B1ON,AN=NB1,
又∵∠MOB1=∠MOB,
∴∠NOM=90°,
∴∠OMN=∠NOB1,
又∵∠OB1M=∠OB1N=∠B=90°,
∴△MB1O∽△OB1N,
∴
| B1O |
| B1M |
| NB1 |
| B1O |
∴OB12=MB1•NB1,
又∵MB1=MB=x,OB1=OB=2,
∴22=x•NB1,
∴NB1=
| 4 |
| x |
∴AN=
| 4 |
| x |
∵AD⊥AB,
∴∠DAB=90°,
又∵∠B=90°,
∴AD∥BC,

∴△CMF∽△ANF,
∴
| C△CMF |
| C△ANF |
| CM |
| AN |
| 4-x | ||
|
| 4x-x2 |
| 4 |
| 1 |
| 4 |
∴y=-
| 1 |
| 4 |
(3)由题意知:∠EAO=∠C=45°
∵△FMC和△AEO相似,
∴只有两种情况:当△FMC∽△AEO时或当△FMC∽△AOE时,
①如图2,当△FMC∽△AEO时,有∠FMC=∠AEO,∠CFM=∠AOE,

可证:∠AOE=∠OMB=∠FMO,
则∠CFM=∠FMO,
∴OM∥AC,
∴∠OMB=∠C=45°,
∴Rt△MOB中,MB=OB•tan45°=2,
②如图3,当△FMC∽△AOE时,
则∠FMC=∠AOE,
∵∠AOE=∠OMB=∠OMF,
∴∠CMF=∠OMF=∠OMB=60°,
∴Rt△MOB中,MB=
| OB |
| tan60° |
2
| ||
| 3 |
所以,综上述,知BM=2或BM=
| 2 |
| 3 |
| 3 |
点评:此题主要考查了相似三角形的判定和性质以及翻折变换的性质和锐角三角函数等知识,根据已知△FMC和△AEO相似进行分类讨论得出是解题关键.

练习册系列答案
相关题目