Question

【题目】如图，△ABC中

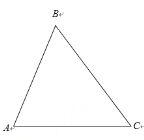
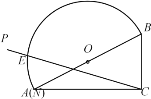
（1）请你利用无刻度的直尺和圆规在平面内画出满足PB2＋PC2＝BC2的所有点P构成的图形，并在所作图形上用尺规确定到边AC、BC距离相等的点P．（作图必须保留作图痕迹）

（2）在（1）的条件下，连接BP，若BC＝15，AC＝14，AB＝13，求BP的长．

Answer 1

【答案】（1）见解析；（2）BP＝

【解析】

（1）根据PB2＋PC2＝BC2得出P点所构成的圆以BC为直径，根据垂直平分线画法画出O点，补全⊙O，再作∠ACB的角平分线与⊙O的交点即是P点.

（2）设⊙O与AC的交点为H，AH＝x，得到AH、BH，根据题意求出OP∥AC，即可得出OP⊥BH，BQ＝BH，OQ=CH,求出PQ，根据勾股定理求出BP.

(1)如图：

（2）由（1）作图，设⊙O与AC的交点为H，连接BH，∴∠BHC＝90°

∵BC＝15，AC＝14，AB＝13

设AH＝x ∴HC＝14－x

∴

解得：x＝5

∴AH＝5

∴BH＝12.

连接OP，由（1）作图知CP平分∠BCA

∴∠PCA＝∠BCP

又∵OP＝OC

∴∠OPC＝∠BCP

∴∠OPC＝∠PCA

∴OP∥CA

∴OP⊥BH 与点Q

∴BQ＝BH＝6

又BO＝

∴OQ＝

∴PQ＝

∴BP＝.