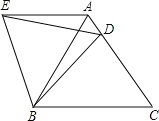
题目内容
【题目】如图，△ABC中，D是BC上一点，E是AC上一点，点G在BE上，联结DG并延长交AE于点F，∠BGD=∠BAD=∠C．
（1）求证：
；
（2）如果∠BAC=90°，求证：AG⊥BE．
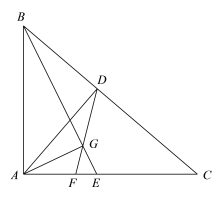
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）由△BDG∽△BEC，可得
，即可推出结论；
（2）由△BAD∽△BCA，推出∠BDA=∠BAC=90°，由∠BAD=∠BGD，推出A，B，D，G四点共圆，推出∠AGB=∠ADB=90°.
（1）证明：∵∠DBG=∠CBE，
∠BGD=∠C，
∴△BDG∽△BEC，
∴，
∴BDBC=BGBE；
（2）∵∠ABD=∠CBA，∠BAD=∠C，
∴△BAD∽△BCA，
∴∠BDA=∠BAC=90°，
∵∠BAD=∠BGD，
∴A，B，D，G四点共圆，
∴∠AGB=∠ADB=90°，
∴AG⊥BE．
练习册系列答案
相关题目
【题目】二次函数y＝ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表给出了以下结论：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
①二次函数y＝ax2+bx+c有最小值，最小值为﹣3；②当﹣
＜x＜2时，y＜0；③二次函数y＝ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴的两侧；④当x＜1时，y随x的增大而减小．则其中正确结论有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
