题目内容
【题目】如图所示，有一条小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是m2 ．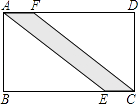 
【答案】240
【解析】解：在矩形ABCD中，AF∥EC， 又AF=EC，
∴四边形AECF是平行四边形．
在Rt△ABE中，AB=60，AE=100，
根据勾股定理得BE=80，
∴EC=BC﹣BE=4，
所以这条小路的面积S=ECAB=4×60=240（m2）．
所以答案是：240．
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
【题目】为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．
组别 | 捐款额（x）元 | 户数 |
A | 1≤x＜50 | a |
B | 50≤x＜100 | 10 |
C | 100≤x＜150 | |
D | 150≤x＜200 | |
E | x≥200 |
请结合以上信息解答下列问题．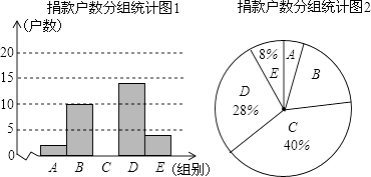
（1）a= ， 本次调查样本的容量是；
（2）补全“捐款户数分组统计表和捐款户数统计图1”；
（3）若该社区有1500户住户，请根据以上信息估计，全社区捐款不少于150元的户数是多少？
