题目内容
已知平行于x轴的直线y=a(a≠0)与函数y=x和函数y= 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0).(1)若a>0,且tan∠POB=
 ,求线段AB的长;
,求线段AB的长;(2)在过A,B两点且顶点在直线y=x上的抛物线中,已知线段AB=
 ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;(3)已知经过A,B,P三点的抛物线,平移后能得到y=
 x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
【答案】分析:(1)设B点坐标为(m,n),利用三角函数求出m与n的值以及点A的坐标.
(2)依题意可知抛物线开口向下,设点A(a,a),B( ,a)求出a值.设二次函数为y=k(x+
,a)求出a值.设二次函数为y=k(x+ 把点A代入求得k值以及函数解析式.
把点A代入求得k值以及函数解析式.
(3)依题意可求出抛物线的对称轴为x=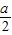 +
+ .把点A的坐标代入解析式求出a值.
.把点A的坐标代入解析式求出a值.
解答:解:(1)设第一象限内的点B(m,n),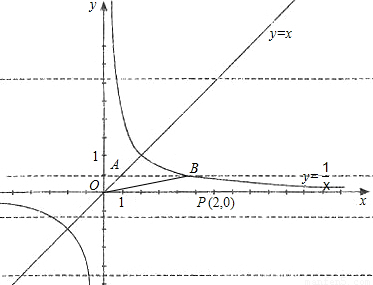
则tan∠POB=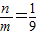 ,
,
得m=9n,
又点B在函数y= 的图象上,得n=
的图象上,得n= ,
,
所以m=3(-3舍去),
点B为(3, ),
),
而AB∥x轴,所以点A( ,
, ),
),
所以AB=3- .
.
(2)由条件可知所求抛物线开口向下,
设点A(a,a),B( ,a),
,a),
则AB= -a=
-a= ,
,
所以3a2+8a-3=0,
解得a=-3或a= .
.
当a=-3时,点A(-3,-3),B(- ,-3),
,-3),
因为顶点在y=x上,
所以顶点为(- ,-
,- ),
),
所以可设二次函数为y=k(x+ )2-
)2- ,
,
点A代入,解得k=- ,
,
所以所求函数解析式为y=- (x+
(x+ )2-
)2-
同理,当a= 时,所求函数解析式为y=-
时,所求函数解析式为y=- (x-
(x- )2+
)2+ ;
;
(3)设A(a,a),B( ,a),由条件可知抛物线的对称轴为x=
,a),由条件可知抛物线的对称轴为x= +
+ ,
,
设所求二次函数解析式为:y= (x-2)(x-(a+
(x-2)(x-(a+ )+2),
)+2),
点A(a,a)代入,
解得a1=3,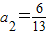 ,
,
所以点P到直线AB的距离为3或 .
.
点评:本题考查的是二次函数的综合运用,较为复杂.
(2)依题意可知抛物线开口向下,设点A(a,a),B(
 ,a)求出a值.设二次函数为y=k(x+
,a)求出a值.设二次函数为y=k(x+ 把点A代入求得k值以及函数解析式.
把点A代入求得k值以及函数解析式.(3)依题意可求出抛物线的对称轴为x=
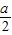 +
+ .把点A的坐标代入解析式求出a值.
.把点A的坐标代入解析式求出a值.解答:解:(1)设第一象限内的点B(m,n),

则tan∠POB=
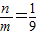 ,
,得m=9n,
又点B在函数y=
 的图象上,得n=
的图象上,得n= ,
,所以m=3(-3舍去),
点B为(3,
 ),
),而AB∥x轴,所以点A(
 ,
, ),
),所以AB=3-
 .
.(2)由条件可知所求抛物线开口向下,
设点A(a,a),B(
 ,a),
,a),则AB=
 -a=
-a= ,
,所以3a2+8a-3=0,
解得a=-3或a=
 .
.当a=-3时,点A(-3,-3),B(-
 ,-3),
,-3),因为顶点在y=x上,
所以顶点为(-
 ,-
,- ),
),所以可设二次函数为y=k(x+
 )2-
)2- ,
,点A代入,解得k=-
 ,
,所以所求函数解析式为y=-
 (x+
(x+ )2-
)2-
同理,当a=
 时,所求函数解析式为y=-
时,所求函数解析式为y=- (x-
(x- )2+
)2+ ;
;(3)设A(a,a),B(
 ,a),由条件可知抛物线的对称轴为x=
,a),由条件可知抛物线的对称轴为x= +
+ ,
,设所求二次函数解析式为:y=
 (x-2)(x-(a+
(x-2)(x-(a+ )+2),
)+2),点A(a,a)代入,
解得a1=3,
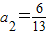 ,
,所以点P到直线AB的距离为3或
 .
.点评:本题考查的是二次函数的综合运用,较为复杂.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
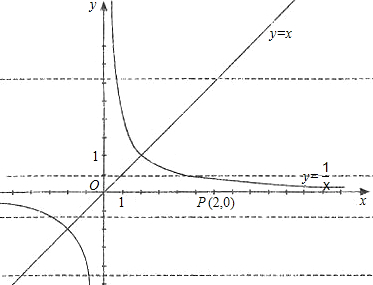
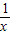 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.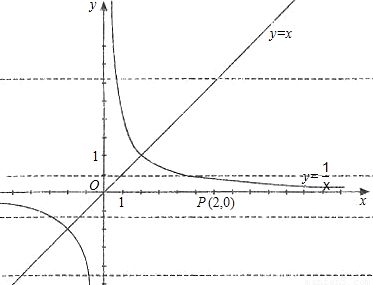
 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
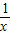 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.