题目内容
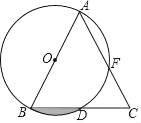
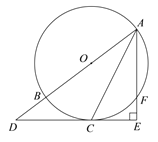
【题目】如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若AE=3,DE=4,求⊙O的半径的长.
【答案】(1)证明见解析;(2)⊙O的半径长为![]() .
.
【解析】
(1)连接OC,证OC∥AE,即可得出OC⊥DE,根据切线判定推出即可.
(2)证△OCD∽△ADE,即可求出DF.
(1)连接![]() ,
,
∵点C为弧BF的中点,
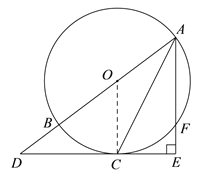
∴弧BC=弧CF.∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵AE⊥DE,
∴![]() .
.
∴![]() .
.
∴OC⊥DE.
∴DE是⊙O的切线.
(2)由勾股定理得AD=5,
∵ ![]() ,
,
∠D=∠D,
∴△OCD∽△AED,
∴![]() ,
,
即![]() ,
,
解得r=![]() ,
,
∴⊙O的半径长为![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.