题目内容
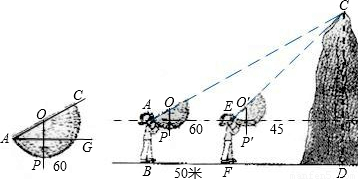
一次数学活动中,小迪利用自己制作的测角器测量小山的高度CD.已知她的眼睛与地面的距离为1.6米,小迪在B处测量时,测角器中的∠AOP=60°(量角器零度线AC和铅垂线OP的夹角,如图);然后她向小山走50米到达点F处(点B,F,D在同一直线上),这时测角器中的∠EO'P'=45°,那么小山的高度CD是多少?(注:数据| 3 |
| 2 |
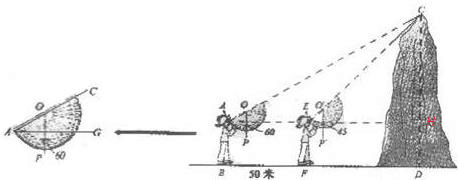
分析:如图,设水平视线与CD交于H点,设CD=x,则CH=x-1.6,解直角三角形分别求AH,EH,根据AH-EH=AE=BF=50,列方程求解.
解答:解:如图,设水平视线与CD交于H点,设CD=x,则CH=x-1.6,
在Rt△CEH中,∠CEH=90°-∠EO'P'=45°,∴EH=CH=(x-1.6),
在Rt△CAH中,∠CAH=90°-∠AOP=30°,∴AH=
CH=
(x-1.6),
∵AH-EH=AE=BF=50,∴
(x-1.6)-(x-1.6)=50,
解得x=25(
+1)+1.6≈69.9.
答:小山的高度CD约为69.9米.
在Rt△CEH中,∠CEH=90°-∠EO'P'=45°,∴EH=CH=(x-1.6),
在Rt△CAH中,∠CAH=90°-∠AOP=30°,∴AH=
| 3 |
| 3 |
∵AH-EH=AE=BF=50,∴
| 3 |
解得x=25(
| 3 |
答:小山的高度CD约为69.9米.
点评:本题考查了解直角三角形的运用.关键是把问题转化到两个直角三角形中,利用公共的直角边表示另外两个直角边,列方程求解.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
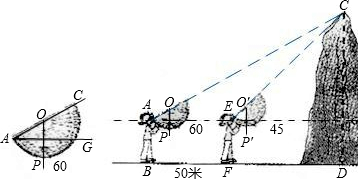
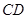 .已知她的眼睛与地面的距离为1.6米,小迪在
.已知她的眼睛与地面的距离为1.6米,小迪在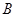 处测量时,测角器中的
处测量时,测角器中的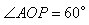 (量角器零度线
(量角器零度线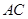 和铅垂线
和铅垂线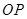 的夹角,如图);然后她向小山走50米到达点
的夹角,如图);然后她向小山走50米到达点 处(点
处(点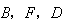 在同一直线上),这时测角器中的
在同一直线上),这时测角器中的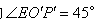 ,那么小山的高度
,那么小山的高度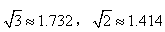 ,供计算时选用)
,供计算时选用)
 ≈1.732,
≈1.732,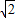 ≈1.414供计算时选用)
≈1.414供计算时选用)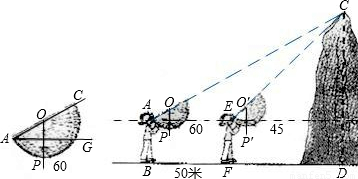
 ≈1.732,
≈1.732,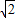 ≈1.414供计算时选用)
≈1.414供计算时选用)