题目内容
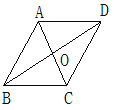
【题目】如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线。
(1)判断∠AOB与∠COD有怎样的数量关系,为什么?
(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?
【答案】(1)∠AOB+∠COD=180°,理由见解析;(2)AB∥CD,理由见解析
【解析】试题分析:(1)本题考查的是角平分线的性质;(2)本题利用角平分线的性质和平行线的判定解决即可.
试题解析:
(1)∠AOB+∠COD=180°
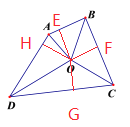
因为:过点O分别作OE⊥AB,OF⊥BC,OG⊥CD,OH⊥AD,∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,∴OE=OF=OG=OH,∴∠AOH=∠AOE, ∠BOF=∠BOE, ∠COF=∠COG, ∠DOG=∠HOD,∴∠AOE+∠BOE+∠COG+∠DOG=∠AOH+∠BOF+ ∠COF+∠HOD,∴∠AOB+∠COD=180°;
(2)AB∥CD.
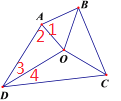
由(1)知∠AOB+∠COD=180°,∴∠COB+∠AOD=180°,∵∠AOD=∠BOC,∴∠AOD=90°,∴∠2+∠3=90°,∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,∴AB∥CD.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目