题目内容
设n是正整数,则 、
、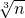 按整数部分的大小可以这样分组:
按整数部分的大小可以这样分组:
整数部分为1: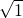 ,
, ,
, ;
; 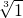 ,
,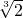 ,…,
,…,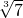 .
.
整数部分为2: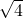 ,
, ,…,
,…,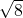 ;
; 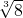 ,
,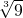 ,…,
,…,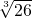 .
.
整数部分为3: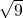 ,
,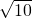 ,…,
,…,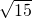 ;
; 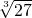 ,
, ,…,
,…,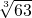 .
.
…
(1)若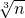 的整数部分4,则n的最小值、最大值分别是多少?
的整数部分4,则n的最小值、最大值分别是多少?
(2)若 的整数部分5,则n可能的值有几种?
的整数部分5,则n可能的值有几种?
解:(1)n的最小值64,n的最大值124;
(2)∵n的最小值25,n的最大值35,
∴n可能的值有11种.
分析:(1)根据规律利用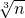 的整数部分4,即可得出答案,
的整数部分4,即可得出答案,
(2)根据规律利用 的整数部分5,即可得出答案.
的整数部分5,即可得出答案.
点评:本题主要考查了根式的计算和性质应用,难度适中.
(2)∵n的最小值25,n的最大值35,
∴n可能的值有11种.
分析:(1)根据规律利用
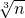 的整数部分4,即可得出答案,
的整数部分4,即可得出答案,(2)根据规律利用
 的整数部分5,即可得出答案.
的整数部分5,即可得出答案.点评:本题主要考查了根式的计算和性质应用,难度适中.

练习册系列答案
相关题目
如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
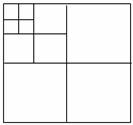
(1)填写下表:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 | 10 |
(2)如果剪了8次,共剪出__ ___个小正方形.
(3)如果剪n(n是正整数)次,共剪出__ __个小正方形.
(4)设最初正方形纸片边长为1,则剪n(n是正整数)次后,最小正方形的边长为__ _.
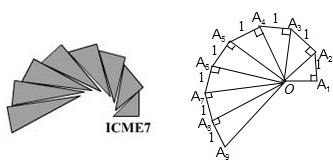 这些线段中长度为正整数的线段有
这些线段中长度为正整数的线段有 、
、 按整数部分的大小可以这样分组:
按整数部分的大小可以这样分组: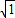 ,
,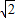 ,
, ;
;  ,
, ,…,
,…,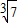 .
. ,
,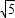 ,…,
,…, ;
;  ,
, ,…,
,…,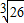 .
.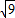 ,
, ,…,
,…,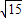 ;
; 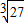 ,
, ,…,
,…, .
. 的整数部分4,则n的最小值、最大值分别是多少?
的整数部分4,则n的最小值、最大值分别是多少?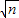 的整数部分5,则n可能的值有几种?
的整数部分5,则n可能的值有几种?