题目内容
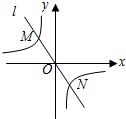 如图,过原点的直线l与反比例函数y=-
如图,过原点的直线l与反比例函数y=-| 1 | x |
分析:欲求MN的长的最小值,由双曲线的对称性知ON=OM,可转化为求OM的最小值,列出OM距离的求解式子,求式子的最小值即可.
解答:解:由题意可设点M的坐标为(x,-
),
则OM=
=
,
∵x2+
-2=(x-
)2≥0,
∴x2+
≥2,由此可得OM的最小值为
,
由双曲线的对称性可知ON=OM,故MN的最小值为2
.
故答案为:2
.
| 1 |
| x |
则OM=
(|x|)2+(-
|
x2+
|
∵x2+
| 1 |
| x2 |
| 1 |
| x |
∴x2+
| 1 |
| x2 |
| 2 |
由双曲线的对称性可知ON=OM,故MN的最小值为2
| 2 |
故答案为:2
| 2 |
点评:本题通过反比例函数的知识,考查学生的猜想探究能力.解题时先直观地猜想,再按照从特殊到一般的方法去验证.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
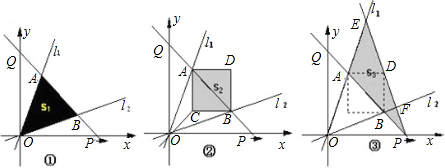
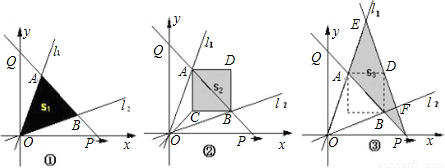
 (2013•滨州)根据要求,解答下列问题:
(2013•滨州)根据要求,解答下列问题: 如图,过原点的直线l与反比例函数
如图,过原点的直线l与反比例函数 x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)
x.点P从原点O出发沿x轴正方向以每秒1个单位长度的速度运动.直线PQ交y轴正半轴于点Q,且分别交l1、l2于点A、B.设点P的运动时间为t秒时,直线PQ的解析式为y=-x+t.△AOB的面积为Sl(如图①).以AB为对角线作正方形ACBD,其面积为S2(如图②).连接PD并延长,交l1于点E,交l2于点F.设△PEA的面积为S3;(如图③)