Question

（本题8分）把两个直角边长均为6的等腰直角三角板ABC和EFG叠放在一起（如图①），使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.

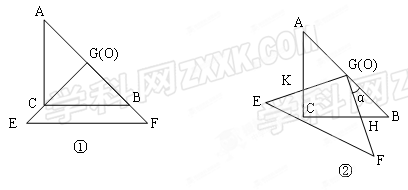
【小题1】(1) 探究：在上述旋转过程中，BH与CK的数量关系以及四边形CHGK的面积的变化情况（直接写出探究的结果，不必写探究及推理过程）；
　　【小题2】(2) 利用（1）中你得到的结论，解决下面问题：连接HK，在上述旋转过程中，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的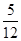？若存在，求出此时BH的长度；若不存在，说明理由.

Answer 1

【小题1】解：(1) BH与CK的数量关系：BH=CK      ……（1分）
四边形CHGK的面积的变化情况：四边形CHGK的面积不变，始终等于9.（说明：答出四边形CHGK的面积不变即可）                                  ………… （2分）
【小题2】(2)假设存在使△GKH的面积恰好等于△ABC面积的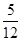的位置，
设BH =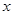，由题意及（1）中结论可得，CK = BH=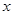，CH = CB-BH =6-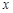，    …………（3分）
∴，
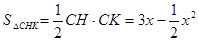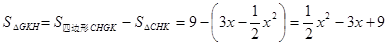∴   …………（5分）
∵△GKH的面积恰好等于△ABC面积的,
∴，
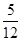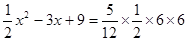解得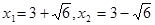，（经检验，均符合题意）           …………（7分）
∴存在使△GKH的面积恰好等于△ABC面积的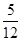的位置，此时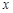的值为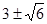（8分）解析:
略