题目内容
A′、B′、C′、D′顺次为四边形ABCD各边的中点，下面条件使四边形A′B′C′D′为正方形的条件是
- A.四边形ABCD是矩形
- B.四边形ABCD是菱形
- C.四边形ABCD是等腰梯形
- D.四边形ABCD中，AC⊥BD，且AC=BD
D
分析：根据正方形、矩形、菱形、等腰梯形的性质．相邻两边的中点的连线段可形成中位线得到线段之间特殊的数量关系和位置关系（平行）．
解答：A、顺次连接矩形的四边中点得到菱形，故A不正确；
B、顺次连接菱形的四边中点得到矩形，故B错误；
C、顺次连接对角线互相垂直的等腰梯形的四边中点才能得到正方形，故C不正确；
D、顺次连接对角线互相垂直且相等的四边形四边中点能得到正方形，故D正确．
故选D．
点评：本题考查了正方形的概念性质和判定，考查了中点四边形，各图形性质及之间的相互联系，对角线之间的关系．
分析：根据正方形、矩形、菱形、等腰梯形的性质．相邻两边的中点的连线段可形成中位线得到线段之间特殊的数量关系和位置关系（平行）．
解答：A、顺次连接矩形的四边中点得到菱形，故A不正确；
B、顺次连接菱形的四边中点得到矩形，故B错误；
C、顺次连接对角线互相垂直的等腰梯形的四边中点才能得到正方形，故C不正确；
D、顺次连接对角线互相垂直且相等的四边形四边中点能得到正方形，故D正确．
故选D．
点评：本题考查了正方形的概念性质和判定，考查了中点四边形，各图形性质及之间的相互联系，对角线之间的关系．
练习册系列答案
相关题目
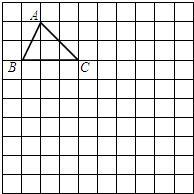21、如图，在10×10正方形网格中，每个小正方形的边长均为1个单位．将△ABC向下平移4个单位，得到△A1B1C1，再把△A1B1C1向右平移3个单位，得到△A2B2C2，再将△A2B2C2绕点C2顺时针旋转90°，得到△A3B3C3，请你画出△A1B1C1，△A2B2C2和△A3B3C3．（不要求写画法）．
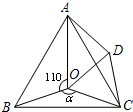18、如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．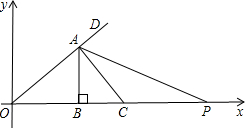
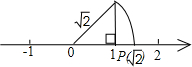如图作一个等腰直角三角形，以数轴的原点为旋转中心，将过原点的斜边顺时针旋转，使斜边的另一端点落在数轴正半轴的点P处，则点P表示的数是
4）．