题目内容
定义一种对正整数n的运算“F”:(1)当n为奇数时,结果为3n+5;
(2)当n为偶数时,结果为
| n |
| 2k |
| n |
| 2k |

那么,当n=1796时,第2010次“F”运算的结果是
分析:先分别计算出n=1796时第一、二、三、四、五、六次、七次运算的结果,找出规律再进行解答即可.
解答:解:根据题意,得
当n=1796时,
第一次运算,
=449;
第二次运算,3n+5=3×449+5=1352;
第三次运算,
=169;
第四次运算,3×169+5=512;
第五次运算,
=1;
第六次运算,3×1+5=8;
第七次运算,
=1,
可以看出,从第五次开始,结果就只是1,8两个数轮流出现,
且当次数为偶数时,结果是8,次数是奇数时,结果是1,
而2010次是偶数,因此最后结果是1.
故答案为:1.
当n=1796时,
第一次运算,
| 1796 |
| 2 2 |
第二次运算,3n+5=3×449+5=1352;
第三次运算,
| 1352 |
| 23 |
第四次运算,3×169+5=512;
第五次运算,
| 512 |
| 29 |
第六次运算,3×1+5=8;
第七次运算,
| 8 |
| 23 |
可以看出,从第五次开始,结果就只是1,8两个数轮流出现,
且当次数为偶数时,结果是8,次数是奇数时,结果是1,
而2010次是偶数,因此最后结果是1.
故答案为:1.
点评:此题考查的是整数的奇偶性,能根据所给条件得出n=1796时七次的运算结果,找出规律是解答此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
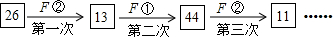 若n=15,则第15次“F”运算的结果是( )
若n=15,则第15次“F”运算的结果是( )
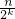 (其中k是使
(其中k是使