题目内容
【题目】D为等腰Rt△ABC斜边AB的中点,DM⊥DN,DM,DN分别交BC,CA于点E,F.
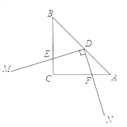
(1)当∠MDN绕点D转动时,求证:DE=DF.
(2)若AB=2,求四边形DECF的面积.
【答案】(1)证明见解析.(2)![]() 。
。
【解析】分析:(1)连CD,根据等腰直角三角形的性质得到CD平分∠ACB,CD⊥AB,∠A=45°,CD=DA,则∠BCD=45°,∠CDA=90°,由DM⊥DN得∠EDF=90°,根据等角的余角相等得到∠CDE=∠ADF,根据全等三角形的判定易得△DCE≌△ADF,即可得到结论;(2)由△DCE≌△ADF,则S△DCE=S△ADF,于是四边形DECF的面积=S△ACD,由而AB=2可得CD=DA=1,根据三角形的面积公式易求得S△ACD,从而得到四边形DECF的面积.
本题解析:
(1)连CD,如图,
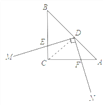
∵D为等腰Rt△ABC斜边AB的中点,
∴CD平分∠ACB,CD⊥AB,∠A=45°,CD=DA,
∴∠BCD=45°,∠CDA=90°,
∵DM⊥DN,
∴∠EDF=90°,
∴∠CDE=∠ADF,
在△DCE和△ADF中,
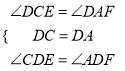 ,
,
∴△DCE≌△ADF(ASA),
∴DE=DF;
(2)∵△DCE≌△ADF,
∴S△DCE=S△ADF,
∴四边形DECF的面积=S△ACD,
而AB=2,
∴CD=DA=1,
∴四边形DECF的面积=S△ACD=![]() CDDA=
CDDA=![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目