题目内容
如图,直线l:y=-x- 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合), 的值是否发生变化?( )
的值是否发生变化?( )
A. | B. | C.2 | D.变化 |

A
解析试题分析:对于直线l:y=-x- ,
,
令x=0,得到y=- ;
;
令y=0,得到x=- ,
,
∴OA=OC,又∠AOC=90°,
∴△OAC为圆内接等腰直角三角形,AC为直径,
如图,在CE上截取CM=AE,连接OM,
∵在△OAE和△OCM中, ,
,
∴△OAE≌△OCM(SAS),
∴∠AOE=∠COM,OM=OE,
∵∠AOC=∠AOM+∠MOC=90°,∠MOE=∠AOE+∠MOC,
∴∠MOE=90°,
∴△OME为等腰直角三角形,
∴ME= EO,
EO,
又∵ME=EC-CM=EC-AE,
∴EC-AE= EO,即
EO,即 =
= .
. 
考点: 一次函数综合题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. | B. | C. | D. |
若y=(m-2)x+(m2-4)是正比例函数,则m的取值是( )
| A.2 | B.-2 | C.±2 | D.任意实数 |
若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(-2,0),则抛物线y=ax2+bx的对称轴为( )
| A.直线x=1 | B.直线x=-2 |
| C.直线x=-1 | D.直线x=-4 |
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
| A.x>-1 | B.x<-1 |
| C.x<-2 | D.无法确定 |
若函数 和
和 有相等的函数值,则
有相等的函数值,则 的值为( )
的值为( )
A. | B. | C.1 | D.  |
 (a≠0)在同一直角坐标系中的图像可能是( )
(a≠0)在同一直角坐标系中的图像可能是( )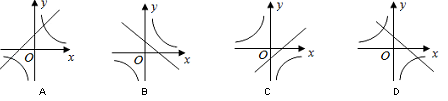
 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米( ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间 的函数关系的大致图象是( ).
的函数关系的大致图象是( ).
 的图象如图所示,则反比例函数
的图象如图所示,则反比例函数 与一次函数
与一次函数 在同一坐标系中的大致图象是( ).
在同一坐标系中的大致图象是( ).