��Ŀ����
��ͼ��ʾ,ij����С��Ҫ��һ��һ�߿�ǽ��ǽ��15m���Ŀյ�����һ�����λ�ABCD,����һ�߿�ǽ,���������ܳ�Ϊ40m��դ��Χ��,������BC�߳�Ϊx��,�������Ϊy��m2��
��1����y��x֮��ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ;
��2�����������Ļ�����ܴﵽ200m2������,�����ʱx��ֵ;������,˵������;
��3����������,�жϵ�xȡ��ֵʱ,����������
��1��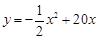 ��0��x��15��;
��0��x��15��;
��2����������ܴﵽ200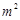 ,���ɼ�����;
,���ɼ�����;
��3����x=15ʱ,��������
���������������1����֪���εij����ܳ��ɱ�ʾ��,���ù�ʽ��ʾ���,����ǽ����x��ȡֵ��Χ;
��2����y=200ʱx��ֵ,�����Ա�����ȡֵ��Χ�ش�����;
��3�����ݺ�����ϵʽ������������ֵ��
�����������1����������ã�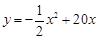 ��0��x��15��
��0��x��15��
��2������
��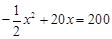 ,��ã�
,��ã�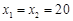 ��15,
��15,
�������ܴﵽ200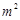 ;
;
��3����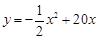 =
=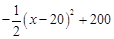
�ຯ��ͼ��Ϊ��20,200���ҿ�������,�൱x��20ʱ,
y��x�����������,��0��x��15
�൱x=15ʱ,y���,��x=15mʱ,��������
���㣺���κ�����Ӧ�ã�

��ϰ��ϵ�д�
 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
�����Ŀ
 ��ͼ���A��-1��-2����B��1��0�����㣮
��ͼ���A��-1��-2����B��1��0�����㣮
 ��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
 x2+bx+c��ͼ��B��C���㣮
x2+bx+c��ͼ��B��C���㣮
 ��ͼ����һ�κ���
��ͼ����һ�κ��� ��ͼ����
��ͼ���� ��
�� ����. C
����. C Ϊ���κ���ͼ��Ķ���.
Ϊ���κ���ͼ��Ķ���.
 ��k >0���뺯��f��ͼ��ֻ����������ʱ����
��k >0���뺯��f��ͼ��ֻ����������ʱ���� ��ֵ.
��ֵ.  ��x�ύ�ڵ�A��B��A��B�ң������е�B������Ϊ��7��0�����������ߵĶ���ΪC��
��x�ύ�ڵ�A��B��A��B�ң������е�B������Ϊ��7��0�����������ߵĶ���ΪC��
