Question

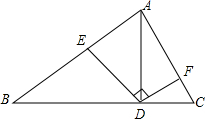如图，AD是Rt△ABC斜边BC上的高，DE⊥DF，且DE和DF分别交AB、AC于E、F．则

AF

AD

=

BE

BD

吗？说说你的理由．

Answer 1

分析：由同角的余角相等，可证得∠B=∠DAC，又由∠EDF=∠BDA，即可证得∠BDE=∠ADF，则可证得△BDE∽△ADF；又由相似三角形的对应边成比例，得到

AF

AD

=

BE

BD

．

解答：解：相等．
理由：∵△ABC中，∠BAC=90°，
∴∠C+∠DAC=90°，∠B+∠C=90°，
∴∠B=∠DAC，
∵DE⊥DF，∠EDF=90°，
∵∠BDA=90°，
∴∠EDF=∠BDA，
∴∠EDF-∠EDA=∠BDA-∠EDA，
∴∠BDE=∠ADF，
∴△BDE∽△ADF，
∴

AF

AD

=

BE

BD

．

点评：此题考查了相似三角形的判定与性质与直角三角形的性质．题目难度不大，解题时需要注意数形结合思想的应用．