ĢāÄæÄŚČŻ
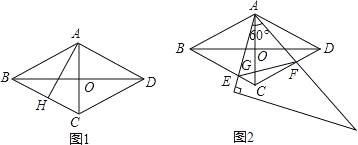
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĮāŠĪABCDÖŠ£¬AC=2£¬”ĻABC=60”ć£¬AC£¬BDĻą½»ÓŚµćO£®
£Ø1£©ČēĶ¼1£¬AH”ĶBC£¬ĒóÖ¤£ŗ”÷ABH”Õ”÷ACH£»
£Ø2£©ČēĶ¼2£¬½«Ņ»øö×ć¹»“óµÄÖ±½ĒČż½Ē°å60”ć½ĒµÄ¶„µć·ÅŌŚĮāŠĪABCDµÄ¶„µćA“¦£¬ČʵćA×óÓŅŠż×Ŗ£¬ĘäÖŠČż½Ē°å60”ć½ĒµÄĮ½±ß·Ö±šÓė±ßBC£¬CDĻą½»ÓŚµćE£¬F£¬Į¬½ÓEFÓėACĻą½»ÓŚµćG£®
¢ŁÅŠ¶Ļ”÷AEFŹĒÄÄŅ»ÖÖĢŲŹāČż½ĒŠĪ£¬²¢ĖµĆ÷ĄķÓÉ£»
¢ŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±µćEĪŖ±ßBCµÄĖĵȷֵ揱£ØBE£¾CE£©£¬ĒóCGµÄ³¤£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»
£Ø2£©¢Ł”÷AEFŹĒµČ±ßČż½ĒŠĪ£¬ĄķÓɼū½āĪö£»¢Ś![]()
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉĮāŠĪµÄŠŌÖŹµĆµ½AB=AC£¬“Ó¶ųÓĆHLÅŠ¶Ø³ö”÷ABH”Õ”÷ACH£®
£Ø2£©ÓÉĮāŠĪµÄŠŌÖŹµĆµ½AB=AC£¬½įŗĻ”ĻABC=60”ćµĆµ½AC=AD£¬ŌŁÅŠ¶Ļ³ö”÷BAC”Õ”÷CAF£¬”÷AEB”Õ”÷EGC¼“æÉ£»
ŹŌĢā½āĪö£ŗ£Ø1£©”ßĖıߊĪABCDŹĒĮāŠĪ£¬ĒŅAC=2£¬”ąAB=BC=2£¬
”ß”ĻABC=60”ć£¬”ą”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬”ąAB=BC=AC=2£¬
”ßAH”ĶBC£¬”ą”ĻABH=”ĻACH=90”ć£¬ŌŚRt”÷ABHŗĶRt”÷ACHÖŠ£¬![]() £¬
£¬
”ą”÷ABH”Õ”÷ACH£ØHL£©£¬
£Ø2£©¢Ł”÷AEFŹĒµČ±ßČż½ĒŠĪ£¬
ĄķÓÉ£ŗ
”ßĖıߊĪABCDŹĒĮāŠĪ£¬ĒŅ”ĻABC=60”ć£¬”ą”÷ABCŗĶ”÷ACDŹĒµČ±ßČż½ĒŠĪ£¬”ą”ĻABC=”ĻBAC=”ĻACD=60”ć£¬
”ß”ĻEAF=60”ć£¬”ą”ĻEAC+”ĻBAE=”ĻEAC+”ĻCAF=60”ć£¬”ą”ĻBAE=”ĻCAF£¬ÓÖ”ßAB=AC£¬
”ą”÷BAC”Õ”÷CAF£¬”ąAE=AF£¬Ó֔ߔĻEAF=60”ć£¬”ą”÷AEFŹĒµČ±ßČż½ĒŠĪ£¬
¢Ś”ß”÷AEFŗĶ”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬”ą”ĻAEF=”ĻABC=”ĻACB=60”ć£¬
”ą”ĻAEB+”ĻBAE=”ĻAEB+”ĻGEC=120”ć£¬”ą”ĻBAE=”ĻGEC£¬”ą”÷AEB”Õ”÷EGC£¬
”ą![]() £¬ÓÖ”ßEC=
£¬ÓÖ”ßEC=![]() BC=
BC=![]() AB£¬”ąCG=
AB£¬”ąCG=![]() BE=
BE=![]() BC=
BC=![]() £®
£®

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø