题目内容
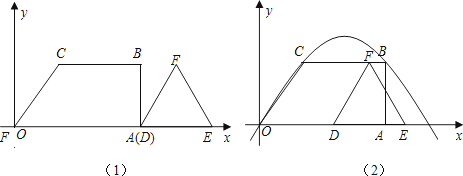
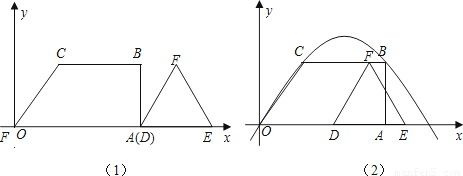
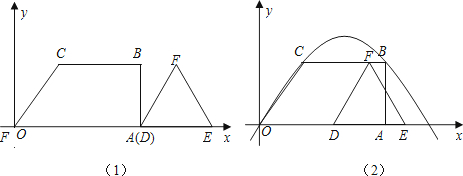
在梯形OABC中,CB∥OA,∠AOC=60°,∠OAB=90°,OC=2,BC=4,以点O为原点,OA所在的直线为x轴,建立平面直角坐标系,另有一边长为2的等边△DEF,DE在x轴上(如图(1)),如果让△DEF以每秒1个单位的速度向左作匀速直线运动,开始时点D与点A重合,当点D到达坐标原点时运动停止.(1)设△DEF运动时间为t,△DEF与梯形OABC重叠部分的面积为S,求S关于t的函数关系式.
(2)探究:在△DEF运动过程中,如果射线DF交经过O、C、B三点的抛物线于点G,是否存在这样的时刻t,使得△OAG的面积与梯形OABC的面积相等?若存在,求出t的值;若不存在,请说明理由.
分析:(1)根据F与B重合前后及E与A重合前后,分三种情况求S关于t的函数关系式;
(2)依题意得D(4-t,0),求出直线OC解析式,根据DF∥OC确定直线DF解析式,再由△OAG的面积与梯形OABC的面积相等,求出G点纵坐标,根据G点在抛物线上求G点横坐标,代入直线DF解析式求t,判断是否符号t的取值范围即可.
(2)依题意得D(4-t,0),求出直线OC解析式,根据DF∥OC确定直线DF解析式,再由△OAG的面积与梯形OABC的面积相等,求出G点纵坐标,根据G点在抛物线上求G点横坐标,代入直线DF解析式求t,判断是否符号t的取值范围即可.
解答:解:(1)依题意得OA=5,
当0≤t<1时,s=
t2,
当1≤t<2时,s=
-
(2-t)2=-
t2+2
t-
,
当2≤t≤5时,s=
;
(2)存在.
依题意,得C(1,
),B(5,
),抛物线对称轴为x=3,
抛物线与x轴两交点坐标为O(0,0),(6,0),
设抛物线解析式为y=ax(x-6),
将C点坐标代入,得a=-
,∴y=-
x(x-6)=-
x2+
x,
由C点坐标可知,直线OC解析式为y=
x,
∵DF∥OC,
∴设直线DF解析式为y=
x+k,
将D(5-t,0)代入得k=
(t-5),
∴直线DF:y=
x+
(t-5),
设△OAG的OA边上高为h,由S△OAG=S梯形OABC,得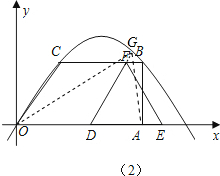
×5×h=
×(4+5)×
,
解得h=
,
将y=
代入y=-
x(x-6)中,得x=3,
∴G(3,
),
代入直线DF:y=
x+
(t-5)中,得t=3.8,
∵0≤t≤5,
∴存在,t=3.8.
当0≤t<1时,s=
| ||
| 2 |
当1≤t<2时,s=
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
当2≤t≤5时,s=
| 3 |
(2)存在.
依题意,得C(1,
| 3 |
| 3 |
抛物线与x轴两交点坐标为O(0,0),(6,0),
设抛物线解析式为y=ax(x-6),
将C点坐标代入,得a=-
| ||
| 5 |
| ||
| 5 |
| ||
| 5 |
6
| ||
| 5 |
由C点坐标可知,直线OC解析式为y=
| 3 |
∵DF∥OC,
∴设直线DF解析式为y=
| 3 |
将D(5-t,0)代入得k=
| 3 |
∴直线DF:y=
| 3 |
| 3 |
设△OAG的OA边上高为h,由S△OAG=S梯形OABC,得

| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得h=
9
| ||
| 5 |
将y=
9
| ||
| 5 |
| ||
| 5 |
∴G(3,
9
| ||
| 5 |
代入直线DF:y=
| 3 |
| 3 |
∵0≤t≤5,
∴存在,t=3.8.
点评:本题考查了二次函数的综合运用.关键是根据直角梯形的特点求顶点坐标,确定抛物线解析式,根据面积关系,列方程求解.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.
如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.