题目内容
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且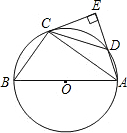 AE⊥CE,连接CD.
AE⊥CE,连接CD.(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
分析:(1)连接OC,求证DC=BC可以证明∠CAD=∠BAC,进而证明
=
;
(2)AB=5,AC=4,根据勾股定理就可以得到BC=3,易证△ACE∽△ABC,则∠DCE=∠BAC,则tan∠DCE的值等于tan∠BAC,在直角△ABC中根据三角函数的定义就可以求出.
 |
| DC |
 |
| BC |
(2)AB=5,AC=4,根据勾股定理就可以得到BC=3,易证△ACE∽△ABC,则∠DCE=∠BAC,则tan∠DCE的值等于tan∠BAC,在直角△ABC中根据三角函数的定义就可以求出.
解答: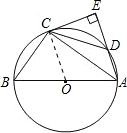 (1)证明:连接OC. (1分)
(1)证明:连接OC. (1分)
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°. (2分)
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. (3分)
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. (4分)
∴
=
.
∴DC=BC. (5分)
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC=
=
=3. (6分)
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC. (7分)
∴
=
.
∴
=
EC=
. (8分)
∵DC=BC=3,
∴ED=
=
=
.(9分)
∴tan∠DCE=
=
=
. (10分)
 (1)证明:连接OC. (1分)
(1)证明:连接OC. (1分)∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°. (2分)
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. (3分)
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. (4分)
∴
 |
| DC |
 |
| BC |
∴DC=BC. (5分)
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC=
| AB2-AC2 |
| 52-42 |
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC. (7分)
∴
| EC |
| BC |
| AC |
| AB |
∴
| EC |
| 3 |
| 4 |
| 5 |
| 12 |
| 5 |
∵DC=BC=3,
∴ED=
| DC2-CE2 |
32-(
|
| 9 |
| 5 |
∴tan∠DCE=
| ED |
| EC |
| ||
|
| 3 |
| 4 |
点评:证明圆的弦相等可以转化为证明弦所对的弧相等,并且本题考查了三角函数的定义,三角函数值只与角的大小有关.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
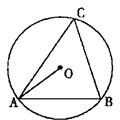 10、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是( )
10、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是( )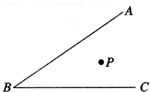 19、如图所示,∠ABC内有一点P,在BA、BC边上各取一点P1、P2,使△PP1P2的周长最小.
19、如图所示,∠ABC内有一点P,在BA、BC边上各取一点P1、P2,使△PP1P2的周长最小.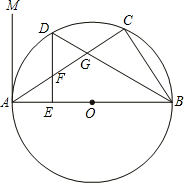 如图所示,△ABC内接于圆O,AB是直径,过A作射线AM,若∠MAC=∠ABC.
如图所示,△ABC内接于圆O,AB是直径,过A作射线AM,若∠MAC=∠ABC.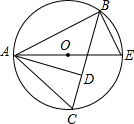 (1)解方程:
(1)解方程: