题目内容
已知一元二次方程ax2+bx+c=0(a≠0)中,其中真命题有
①若a+b+c=0,则b2-4ac≥0;②若方程ax2+bx+c=0两根为-1和2,则2a+c=0;③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根.
- A.1个
- B.2个
- C.3个
- D.0个
C
分析:①a+b+c=0,即系数和为0,说明原方程有一根是1,a≠0,说明原方程为一元二次方程,一元二次方程有根,就有两个,△≥0;
②已知方程两根的值,可利用两根关系的式子变形,得出结论;
③判断方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了.
解答:①若a+b+c=0,方程ax2+bx+c=0有一根为1,又a≠0,则b2-4ac≥0,正确;
②由两根关系可知,-1×2= ,整理得:2a+c=0,正确;
,整理得:2a+c=0,正确;
③若方程ax2+c=0有两个不相等的实根,则-ac>0,可知b2-4ac>0,故方程ax2+bx+c=0必有两个不相等的实根,正确.
正确命题有三个,故选C.
点评:本题考查一元二次方程根的判别式与方程系数的关系,同时考查了学生的综合应用能力及推理能力.
分析:①a+b+c=0,即系数和为0,说明原方程有一根是1,a≠0,说明原方程为一元二次方程,一元二次方程有根,就有两个,△≥0;
②已知方程两根的值,可利用两根关系的式子变形,得出结论;
③判断方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了.
解答:①若a+b+c=0,方程ax2+bx+c=0有一根为1,又a≠0,则b2-4ac≥0,正确;
②由两根关系可知,-1×2=
 ,整理得:2a+c=0,正确;
,整理得:2a+c=0,正确;③若方程ax2+c=0有两个不相等的实根,则-ac>0,可知b2-4ac>0,故方程ax2+bx+c=0必有两个不相等的实根,正确.
正确命题有三个,故选C.
点评:本题考查一元二次方程根的判别式与方程系数的关系,同时考查了学生的综合应用能力及推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
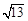 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;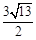 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由. 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;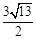 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.