题目内容
如图,一次函数的图象与反比例函数的图象交于A,B两点,与x轴交于点C,过A作AD⊥x轴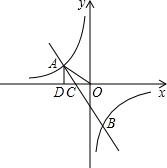 于D,若OA=
于D,若OA=| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)求A点的坐标及反比例函数的解析式;
(2)求一次函数的解析式及△AOB的面积;
(3)在反比例函数的图象上是否存在点P使△OAP为等腰三角形?若存在,请写出P点的坐标;若不存在,请说明理由.
分析:(1)由AD=
OD,设AD=x,则OD=2x,又OA的长,在直角三角形AOD中,根据勾股定理列出关于x的方程,求出方程的解即可得到x的值,确定出AD与DC的长,进而得到A的坐标,设出反比例解析式,把A的坐标代入即可确定出解析式;
(2)把B的横坐标代入(1)中求出的反比例解析式,求出B的纵坐标,确定出B的坐标,设出一次函数的解析式,把A和B的坐标代入即可确定出解析式,然后令解析式中y=0求出x的值,进而得到OC的长,而OC把三角形AOB分为两个三角形,底边都为OC,高为A和B的纵坐标,根据三角形的面积公式即可求出△AOB的面积;
(3)存在,因为反比例函数图象关于y=-x对称,所以找出A关于y=-x的对称点的坐标即为满足题意的点P1的坐标;同理分别找出A和P1关于原点的对称点即为P2,P3的坐标.
| 1 |
| 2 |
(2)把B的横坐标代入(1)中求出的反比例解析式,求出B的纵坐标,确定出B的坐标,设出一次函数的解析式,把A和B的坐标代入即可确定出解析式,然后令解析式中y=0求出x的值,进而得到OC的长,而OC把三角形AOB分为两个三角形,底边都为OC,高为A和B的纵坐标,根据三角形的面积公式即可求出△AOB的面积;
(3)存在,因为反比例函数图象关于y=-x对称,所以找出A关于y=-x的对称点的坐标即为满足题意的点P1的坐标;同理分别找出A和P1关于原点的对称点即为P2,P3的坐标.
解答:解:(1)设AD=x,则OD=2x,又OA=
,
在Rt△AOD中,根据勾股定理得:AD2+OD2=AO2,
即x2+(2x)2=(
)2,
化简得:5x2=5,解得x=1或x=-1(舍去),
所以AD=1,OD=2,
则A的坐标为(-2,1),
设反比例解析式为y=
(k≠0),
把A的坐标代入反比例解析式得:k=-2,
则反比例函数的解析式为y=-
;
(2)把B的横坐标x=
代入反比例解析式y=-
得:y=-4,
所以B的坐标为(
,-4),又A(-2,1),
设直线AB的解析式为:y=kx+b,
将A和B的坐标代入解析式得:
,
解得:
,
则直线AB的解析式为:y=-2x-3,
令y=0,解得x=-
,则C(-
,0),故OC=
,
则S△AOB=S△AOC+S△BOC=
OC•|yA的纵坐标|+
OC•|yB的纵坐标|
=
×
×1+
×
×|-4|=
;
(3)存在.
∵A(-2,1),且反比例函数图象关于y=-x对称,
∴当P与A关于y=-x对称时,△OAP为等腰三角形,此时P1(-1,2);
当P与P1关于原点对称时,△OAP为等腰三角形,此时P2(1,-2);
当P与P2关于y=-x对称时,P3(2,-1),O、A、P三点共线,△OAP不能为等腰三角形.
| 5 |
在Rt△AOD中,根据勾股定理得:AD2+OD2=AO2,
即x2+(2x)2=(
| 5 |
化简得:5x2=5,解得x=1或x=-1(舍去),
所以AD=1,OD=2,
则A的坐标为(-2,1),
设反比例解析式为y=
| k |
| x |
把A的坐标代入反比例解析式得:k=-2,
则反比例函数的解析式为y=-
| 2 |
| x |
(2)把B的横坐标x=
| 1 |
| 2 |
| 2 |
| x |
所以B的坐标为(
| 1 |
| 2 |
设直线AB的解析式为:y=kx+b,
将A和B的坐标代入解析式得:
|
解得:
|
则直线AB的解析式为:y=-2x-3,
令y=0,解得x=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
则S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
(3)存在.
∵A(-2,1),且反比例函数图象关于y=-x对称,
∴当P与A关于y=-x对称时,△OAP为等腰三角形,此时P1(-1,2);
当P与P1关于原点对称时,△OAP为等腰三角形,此时P2(1,-2);
当P与P2关于y=-x对称时,P3(2,-1),O、A、P三点共线,△OAP不能为等腰三角形.
点评:此题考查了勾股定理,待定系数法求反比例解析式及一次函数解析式,以及点关于y=-x及关于原点对称点的求法,要求学生掌握反比例函数的图象与性质,在(2)求三角形面积时注意把三角形分为两个同底的三角形,结合点A和B的纵坐标,利用三角形的面积公式作出解答;第(3)问题注意把所求问题转化为求对称点的问题,找对称点的方法为:(a,b)关于y=-x的对称点坐标为(-b,-a),关于原点对称点的坐标为(-a,-b),进而利用对称的思想解决问题,同时注意把满足题意的点找全.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知反比例函数y=
如图,已知反比例函数y=
 解答:
解答:
