题目内容
已知关于x的方程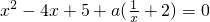 ,若a为正实数,则下列判断正确的是
,若a为正实数,则下列判断正确的是
- A.有三个不等实数根
- B.有两个不等实数根
- C.有一个实数根
- D.无实数根
C
分析:先整理方程,把方程的解转化为二次函数y=x2-4x+5与y=-a( +2)的图象交点问题,然后在同一平面直角坐标系内画出大致图象即可得解.
+2)的图象交点问题,然后在同一平面直角坐标系内画出大致图象即可得解.
解答: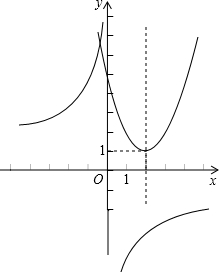 解:方程可化为x2-4x+5=-a(
解:方程可化为x2-4x+5=-a( +2),
+2),
所以,方程的解的个数等于函数y=x2-4x+5与y=-a( +2)的交点的个数,
+2)的交点的个数,
函数y=x2-4x+5的图象经过第一、二象限,
∵a是正实数,
∴-a是负实数,
∴y=-a( +2)的图象位于第二、四象限,
+2)的图象位于第二、四象限,
两个函数图象一定有一个交点,
∴方程有一个实数根.
故选C.
点评:本题考查了二次函数图象与反比例函数图象,把方程的解的个数转化为两个函数图象的交点的个数,正确分析作出函数的大致图象是解题的关键.
分析:先整理方程,把方程的解转化为二次函数y=x2-4x+5与y=-a(
 +2)的图象交点问题,然后在同一平面直角坐标系内画出大致图象即可得解.
+2)的图象交点问题,然后在同一平面直角坐标系内画出大致图象即可得解.解答:
 解:方程可化为x2-4x+5=-a(
解:方程可化为x2-4x+5=-a( +2),
+2),所以,方程的解的个数等于函数y=x2-4x+5与y=-a(
 +2)的交点的个数,
+2)的交点的个数,函数y=x2-4x+5的图象经过第一、二象限,
∵a是正实数,
∴-a是负实数,
∴y=-a(
 +2)的图象位于第二、四象限,
+2)的图象位于第二、四象限,两个函数图象一定有一个交点,
∴方程有一个实数根.
故选C.
点评:本题考查了二次函数图象与反比例函数图象,把方程的解的个数转化为两个函数图象的交点的个数,正确分析作出函数的大致图象是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。 ,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。
,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求ΔABC的周长。