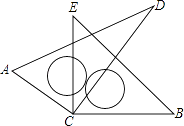题目内容
【题目】已知如图,以正方形ABCD的对角线为边作菱形AEFC,若点B、E、F在同一直线上,求∠EAB的度数. 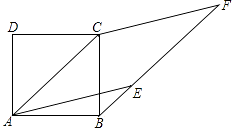
【答案】解:如图,连接BD与AC相交于O,过点E作EH⊥AC于H, 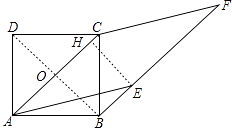 ∵四边形ABCD是正方形,四边形ACFE是菱形,
∵四边形ABCD是正方形,四边形ACFE是菱形,
∴AC⊥BD,AC∥BF,
∴四边形OBEH是矩形,
∴EH=OB= ![]() AC=
AC= ![]() BD,
BD,
∵四边形ACFE是菱形,
∴AC=AE,
∴EH= ![]() AE,
AE,
∴∠HAE=30°,
∵四边形ABCD是正方形,
∴∠CAB=45°,
∴∠EAB=∠CAB﹣∠HAE=15°
【解析】连接BD与AC相交于O,过点E作EH⊥AC于H,可得四边形OBEH是矩形,根据矩形的对边相等可得EH=OB,再根据菱形的四条边都相等可得BD=AE,然后求出EH= ![]() AE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠HAE=30°,根据正方形性质求出∠CAB,即可求出答案.
AE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠HAE=30°,根据正方形性质求出∠CAB,即可求出答案.
【考点精析】本题主要考查了菱形的性质和正方形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】老师想知道某校学生每天上学路上要花多少时间,于是随机选取30名同学每天来校的大致时间(单位:分钟)进行统计,统计表如下:
时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
(1)写出这组数据的中位数和众数;
(2)求这30名同学每天上学的平均时间.