Question

【题目】（发现与思考）如图①∠ACB＝∠ADB＝90°那么点D在经过A，B，C三点的圆上，如图②，如果∠ACB＝∠ADB＝α（α≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上？

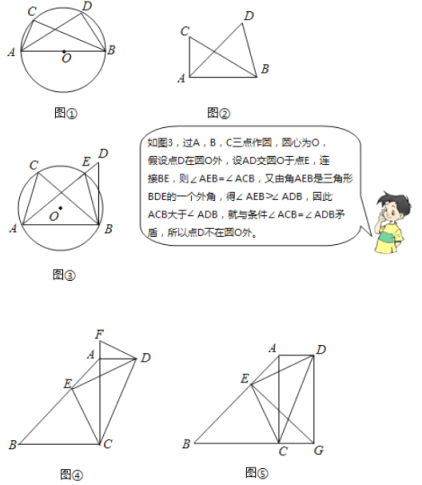
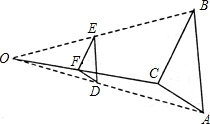
（应用）若四边形ABCD中，AD∥BC，∠CAD＝90°，点E在边AB上，CE⊥DE．

（1）作∠ADF＝∠AED，交CA的延长线于点F（如图④），求证：DF为Rt△ACD的外接圆的切线；

（2）如图⑤，点G在BC的延长线上，∠BGE＝∠BAC，已知sin∠AED＝，AD＝1，求DG的长．

Answer 1

【答案】发现与思考:点D即不在⊙O内，也不在⊙O外，点D在⊙O上；应用:（1）见解析；（2）DG＝2．

【解析】

发现与思考：假设点D在⊙O内，利用圆周角定理及三角形外角的性质，可证得与条件相矛盾的结论，从而可得点D在⊙O上；
应用：（1）作出Rt△ACD的外接圆，由发现与思考可得点E在⊙O上，则可证得∠ACD＝∠FDA，又因为∠ACD＋∠ADC＝90°，于是有∠FDA＋∠ADC＝90°，即可证得DF为Rt△ACD的外接圆的切线；
（2）根据发现与思考可得点G在过C、A、E三点的圆上，即⊙O，进而易证四边形ACGD是矩形，根据已知条件解直角三角形ACD可得AC的长，即DG的长．

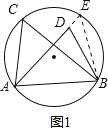
解：发现与思考：如图1，假设点D在⊙O内，延长AD交⊙O于点E，连接BE，则∠AEB＝∠ACB，

∵∠ADB是△BDE的外角，

∴∠ADB＞∠AEB，

∴∠ADB＞∠ACB，

因此，∠ADB＞∠ACB与条件∠ACB＝∠ADB矛盾，

所以点D也不在⊙O内，

因为点D即不在⊙O内，也不在⊙O外，

所以点D在⊙O上；

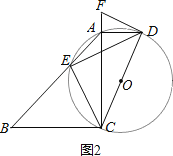
应用：（1）如图2，取CD的中点O，则点O是Rt△ACD的外心，

∵∠CAD＝∠DEC＝90°，

∴点E在⊙O上，

∴∠ACD＝∠AED，

∵∠FDA＝∠AED，

∴∠ACD＝∠FDA，

∵∠DAC＝90°，

∴∠ACD+∠ADC＝90°，

∴∠FDA+∠ADC＝90°，

∴OD⊥DF，

∴DF为Rt△ACD的外接圆的切线；

（2）∵∠BGE＝∠BAC，

∴点G在过C、A、E三点的圆上，如图3，

又∵过C、A、E三点的圆是Rt△ACD的外接圆，即⊙O，

∴点G在⊙O上，

∵CD是直径，

∴∠DGC＝90°，

∵AD∥BC，

∴∠ADG＝90°

∵∠DAC＝90°

∴四边形ACGD是矩形，

∴DG＝AC，

∵sin∠AED＝，∠ACD＝∠AED，

∴sin∠ACD＝，

在Rt△ACD中，AD＝1，

∴CD＝3，

∴AC＝ ，

∴DG＝AC＝．