题目内容
【题目】已知:△ABC内接于⊙O,过点A作直线EF. 
(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
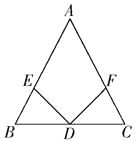
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.
【答案】
(1)AB⊥EF、;∠BAE=90°;∠ABC=∠EAC
(2)证明:如图2,作直径AD,连结CD,

∵AD为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠D=∠B,∠CAE=∠B,
∴∠CAE=∠D,
∴∠EAC+∠CAD=90°,
∴AD⊥EF,
∴EF为⊙O的切线;
(3)如图3,作直径AD,连结CD,BD,

∵AD为直径,
∴∠ABD=90°,
∵∠CAE=∠ABC,
∴∠DAE+∠DAC=∠ABD+∠DBC,
而∠DAC=∠DBC,
∴∠DAE=∠ABD=90°,
∴AD⊥EF,
∴EF为⊙O的切线.
【解析】(1)解:当AB⊥EF或∠BAE=90°可判断EF为⊙O的切线; 当∠ABC=∠EAC,∵AB为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF为⊙O的切线;
所以答案是AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目