Question

【题目】如图，顶点为A（ ，1）的抛物线经过坐标原点O，与x轴交于点B．

（1）求抛物线对应的二次函数的表达式；
（2）过B作OA的平行线交y轴于点C，交抛物线于点D，求证：△OCD≌△OAB；
（3）在x轴上找一点P，使得△PCD的周长最小，求出P点的坐标．

Answer 1

【答案】
（1）

∵抛物线顶点为A（ ，1），

设抛物线解析式为y=a（x﹣ ）2+1，

将原点坐标（0，0）在抛物线上，

∴0=a（ ）2+1

∴a=﹣ ．

∴抛物线的表达式为：y=﹣ x2+ x．

（2）

令y=0，得 0=﹣ x2+ x，

∴x=0（舍），或x=2

∴B点坐标为：（2 ，0），

设直线OA的表达式为y=kx，

∵A（ ，1）在直线OA上，

∴ k=1，

∴k= ，

∴直线OA对应的一次函数的表达式为y= x．

∵BD∥AO，

设直线BD对应的一次函数的表达式为y= x+b，

∵B（2 ，0）在直线BD上，

∴0= ×2 +b，

∴b=﹣2，

∴直线BD的表达式为y= x﹣2．

由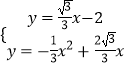

得交点D的坐标为（﹣ ，3），

令x=0得，y=﹣2，

∴C点的坐标为（0，﹣2），

由勾股定理，得：OA=2=OC，AB=2=CD，OB=2 =OD．

在△OAB与△OCD中，

，

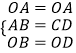∴△OAB≌△OCD．

（3）

点C关于x轴的对称点C'的坐标为（0，2），

∴C'D与x轴的交点即为点P，它使得△PCD的周长最小．

过点D作DQ⊥y，垂足为Q，

∴PO∥DQ．

∴△C'PO∽△C'DQ．

∴ ，

∴ ，

∴PO= ，

∴点P的坐标为（﹣ ，0）．

【解析】（1）用待定系数法求出抛物线解析式，（2）先求出直线OA对应的一次函数的表达式为y= x．再求出直线BD的表达式为y= x﹣2．最后求出交点坐标C，D即可；（3）先判断出C'D与x轴的交点即为点P，它使得△PCD的周长最小．作辅助线判断出△C'PO∽△C'DQ即可．此题是二次函数综合题，主要考查了待定系数法求函数解析式，全等三角形的性质和判定，相似三角形的性质和全等，解本题的关键是确定函数解析式．
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．