题目内容
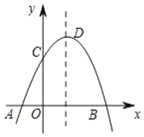
【题目】如图，抛物线y＝﹣x2+2x+3交x轴于A，B两点，交y轴于点C，点D为抛物线的顶点，点C关于抛物线的对称轴的对称点为E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为_____．
【答案】
+
【解析】
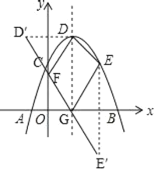
根据抛物线解析式求得点D（1，4）、点E（2，3），作点D关于y轴的对称点D′（-1，4）、作点E关于x轴的对称点E′（2，-3），从而得四边形EDFG的周长=DE+DF+FG+GE=DE+D′F+FG+GE′，当点D′、F、G、E′四点共线时，周长最短，据此根据两点间的距离公式可得答案．
解：如图，
在y＝﹣x2+2x+3中，当x＝0时，y＝3，即点C（0，3），
∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴对称轴为x＝1，顶点D（1，4），
则点C关于对称轴的对称点E的坐标为（2，3），
作点D关于y轴的对称点D′（﹣1，4），作点E关于x轴的对称点E′（2，﹣3），
连接D′、E′，D′E′与x轴的交点G、与y轴的交点F即为使四边形EDFG的周长最小的点，
四边形EDFG的周长＝DE+DF+FG+GE
＝DE+D′F+FG+GE′
＝DE+D′E′
＝
.
∴四边形EDFG的周长的最小值为： +．
故答案是： +．
练习册系列答案
相关题目
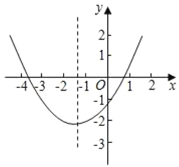
【题目】已知二次函数的解析式是y＝x2﹣2x﹣3．
（1）与y轴的交点坐标是 ，顶点坐标是 ．
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）结合图象回答：当﹣2＜x＜2时，函数值y的取值范围是 ．
