题目内容
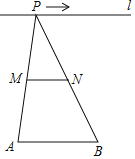
【题目】如图,直线![]() ,连接
,连接![]() ,
,![]() 为一动点.
为一动点.
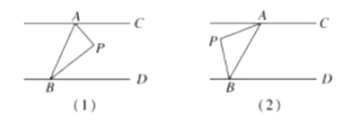
(1)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,求证:
,求证:![]() ;
;
(2)当动点![]() 落在如图
落在如图![]() 所示的位置时,连接
所示的位置时,连接![]() ,则
,则![]() 之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
【答案】(1)见解析(2)∠APB+∠PAC+∠PBD=360![]()
【解析】
(1)延长AP交BD于M,根据三角形外角性质和平行线性质得出∠APB=∠AMB+∠PBD,∠PAC=∠AMB,代入求出即可;
(2)过P作EF∥AC,根据平行线性质得出∠PAC+∠APF=180![]() ,∠PBD+∠BPF=180
,∠PBD+∠BPF=180![]() ,即可得出答案.
,即可得出答案.
(1)延长AP交BD于M,如图1,
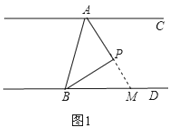
∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)∠APB+∠PAC+∠PBD=360![]() ,
,
如图2,过P作EF∥AC,
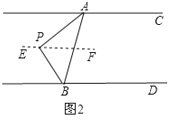
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180![]() ,∠PBD+∠BPF=180
,∠PBD+∠BPF=180![]() ,
,
∴∠PAC+∠APF+∠PBD+∠BPF=360![]() ,
,
∴∠APB+∠PAC+∠PBD=360![]() ,
,
∴∠APB+∠PAC+∠PBD=360![]() .
.

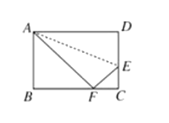
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
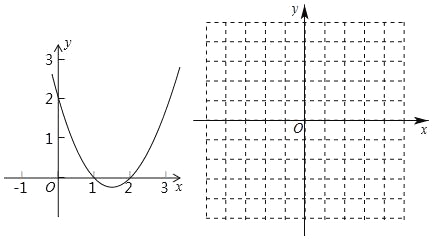
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.