题目内容
在毕业晚会上,同学们表演哪一类型的节目由自己摸球来决定.在一个不透明的口袋中,装有除标号外其它完全相同的A、B、C三个小球,表演节目前,先从袋中摸球一次(摸球后又放回袋中),如果摸到的是A球,则表演唱歌;如果摸到的是B球,则表演跳舞;如果摸到的是C球,则表演朗诵.(1)请用列表或画树状图表示两次摸球的所有可能的结果;
(2)若小明要表演两个节目,则他表演的节目不是同一类型的概率是多少?
分析:根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
解答:解:(1)画树状图如下:
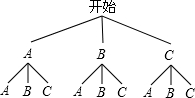
(2)共有9种等可能的结果,不是同一类型的有6种,所以P(不是同一类型)=
=
.

(2)共有9种等可能的结果,不是同一类型的有6种,所以P(不是同一类型)=
| 6 |
| 9 |
| 2 |
| 3 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目