题目内容
【题目】如图,在平面直角坐标系xOy,已知二次函数y=﹣![]() x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
(1)求二次函数的表达式;
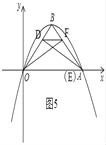
(2)若C是BO的中点,点Q在线段AB上,设点B关于直线CQ的对称点为B',当△OCB'为等边三角形时,求BQ的长度;
(3)若点D在线段BO上,OD=2DB,点E、F在△OAB的边上,且满足△DOF与△DEF全等,求点E的坐标.

【答案】(1)二次函数的表达式为y=﹣![]() x2+2x;(2)BQ=
x2+2x;(2)BQ=![]() ;(3)点E的坐标为:(
;(3)点E的坐标为:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).
【解析】试题分析:(1)利用待定系数法求二次函数的表达式;
(2)先求出OB和AB的长,根据勾股定理的逆定理证明∠ABO=90°,由对称计算∠QCB=60°,利用特殊的三角函数列式可得BQ的长;
(3)因为D在OB上,所以F分两种情况:
i)当F在边OA上时,ii)当点F在AB上时,
当F在边OA上时,分三种情况:
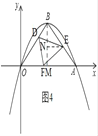
①如图2,过D作DF⊥x轴,垂足为F,则E、F在OA上,②如图3,作辅助线,构建△OFD≌△EDF≌△FGE,③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E;当点F在OB上时,过D作DF∥x轴,交AB于F,连接OF与DA,依次求出点E的坐标即可.
试题解析:(1)将点A的坐标代入二次函数的解析式得:﹣![]() ×42+4b=0,解得b=2,
×42+4b=0,解得b=2,
∴二次函数的表达式为y=﹣![]() x2+2x.
x2+2x.
(2)∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣2)2+2,
(x﹣2)2+2,
∴B(2,2),抛物线的对称轴为x=2.
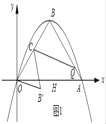
如图1所示:
由两点间的距离公式得:OB=![]() =2
=2![]() ,BA=
,BA=![]() =2
=2![]() .
.
∵C是OB的中点,
∴OC=BC=![]() .
.
∵△OB′C为等边三角形,
∴∠OCB′=60°.
又∵点B与点B′关于CQ对称,
∴∠B′CQ=∠BCQ=60°.
∵OA=4,OB=2![]() ,AB=2
,AB=2![]() ,
,
∴OB2+AB2=OA2,
∴∠OBA=90°.
在Rt△CBQ中,∠CBQ=90°,∠BCQ=60°,BC=![]() ,
,
∴tan60°=![]() ,
,
∴BQ=![]() CB=
CB=![]() ×
×![]() =
=![]() .
.
(3)分两种情况:
i)当F在边OA上时,
①如图2,过D作DF⊥x轴,垂足为F,
∵△DOF≌△DEF,且E在线段OA上,
∴OF=FE,
由(2)得:OB=2![]() ,
,
∵点D在线段BO上,OD=2DB,
∴OD=![]() OB=
OB=![]() ,
,
∵∠BOA=45°,
∴cos45°=![]() ,
,
∴OF=ODcos45°=![]() =
=![]() ,
,
则OE=2OF=![]() ,
,
∴点E的坐标为(![]() ,0);
,0);
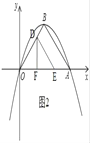
②如图3,过D作DF⊥x轴于F,过D作DE∥x轴,交AB于E,连接EF,过E作EG⊥x轴于G,
∴△BDE∽△BOA,
∴![]() =
=![]() ,
,
∵OA=4,
∴DE=![]() ,
,
∵DE∥OA,
∴∠OFD=∠FDE=90°,
∵DE=OF=![]() ,DF=DF,
,DF=DF,
∴△OFD≌△EDF,
同理可得:△EDF≌△FGE,
∴△OFD≌△EDF≌△FGE,
∴OG=OF+FG=OF+DE=![]() +
+![]() =
=![]() ,EG=DF=ODsin45°=
,EG=DF=ODsin45°=![]() ,
,
∴E的坐标为(![]() ,
,![]() );
);
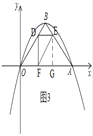
③如图4,将△DOF沿边DF翻折,使得O恰好落在AB边上,记为点E,
过B作BM⊥x轴于M,过E作EN⊥BM于N,
由翻折的性质得:△DOF≌△DEF,
∴OD=DE=![]() ,
,
∵BD=![]() OD=
OD=![]() ,
,
∴在Rt△DBE中,由勾股定理得:BE=![]() =
=![]() ,
,
则BN=NE=BEcos45°=![]() ×
×![]() =
=![]() ,
,
OM+NE=2+![]() ,BM﹣BN=2﹣
,BM﹣BN=2﹣![]() ,
,
∴点E的坐标为:(2+![]() ,2﹣
,2﹣![]() );
);
ii)当点F在AB上时,
过D作DF∥x轴,交AB于F,连接OF与DA,
∵DF∥x轴,
∴△BDF∽△BOA,
∴![]() ,
,
由抛物线的对称性得:OB=BA,
∴BD=BF,
则∠BDF=∠BFD,∠ODF=∠AFD,
∴OD=OB﹣BD=BA﹣BF=AF,
则△DOF≌△DAF,
∴E和A重合,则点E的坐标为(4,0);
综上所述,点E的坐标为:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).

 轻松暑假总复习系列答案
轻松暑假总复习系列答案